https://github.com/takp/bayesian-linear-regression

Sample program to model the data by (normal) linear regression and Bayesian lineaer regression.
https://github.com/takp/bayesian-linear-regression

bayesian-lineaer-regression linear-regression

Last synced: about 1 month ago
JSON representation

Sample program to model the data by (normal) linear regression and Bayesian lineaer regression.

• Host: GitHub
• URL: https://github.com/takp/bayesian-linear-regression
• Owner: takp
• Created: 2014-11-24T11:40:58.000Z (over 10 years ago)
• Default Branch: master
• Last Pushed: 2014-11-24T12:43:29.000Z (over 10 years ago)
• Last Synced: 2023-08-06T04:09:10.714Z (almost 2 years ago)
• Topics: bayesian-lineaer-regression, linear-regression
• Language: Python
• Size: 211 KB
• Stars: 10
• Watchers: 5
• Forks: 5
• Open Issues: 1
• Metadata Files:
  • Readme: README.md

Awesome Lists containing this project

README

        
# Bayesian Linear Regression

Sample program to model the data by (normal) linear regression and Bayesian lineaer regression.

And show the graph to compare those two.

### Environment

- Python 2.7.6

- Numpy

- Matplotlib

### Run

	$ python bayesian_lr.py

### Graph

- Green: Normal linear regression

- Blue:  Bayesian linear regression

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/graph.png)

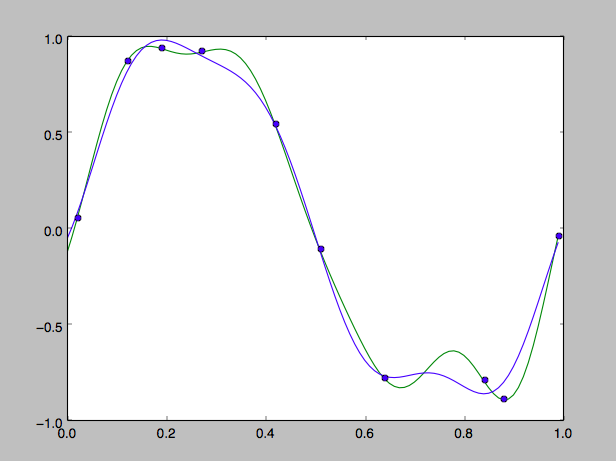
### Logic

The function is as following in general :

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/general_function.jpg)

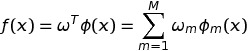
Use the "Gaussian distribution" as the basis function.

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/gaussian.jpg)

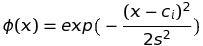
Assuming s = 0.1, c_i = [0.0, 0.1, ..., 1.0]. 

**(1) Normal linear regression**

These "omega" can be solved by this equation.

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/omega_equation.jpg)

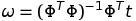
**(2) Bayesian linear regression**

The posterior distribution is expressed as following.

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/posterior_1.jpg)  

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/posterior_2.jpg)  

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/posterior_3.jpg)

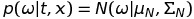
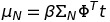
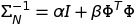
The posterior distribution is Gaussian distribution, so the most possible value is :

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/omega_bayesian.jpg)

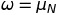
So, it is possible to figure out the function by calculating Mu_N.

This time, I assume alpha = 0.1, beta = 9.0.

Phi is the matrix as following.

![Graph](https://raw.githubusercontent.com/takp/bayesian-linear-regression/master/images/Phi.jpg)

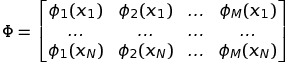
### Numpy

- numpy.linalg.solve : Sove a linear matrix equation. 

  ref. http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.solve.html

- numpy.dot : Scalar product, Inner product

  ref. http://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html

- numpy.linalg.inv : 

- numpy.append :

### Reference

(in Japanese) http://gihyo.jp/dev/serial/01/machine-learning/0014?page=1