Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/tatevkaren/multivariate-statistics
Case Study in ranking U.S. cities based on a single linear combination of rating variables. Dimensionality techniques used in the analysis are Principal Component Analysis (PCA), Factor Analysis (FA), Canonical Correlation Analysis (CCA)
https://github.com/tatevkaren/multivariate-statistics
canonical-correlation-analysis dimensionality-reduction factor-analysis multivariate-analysis multivariate-statistics principal-component-analysis
Last synced: 15 days ago
JSON representation
Case Study in ranking U.S. cities based on a single linear combination of rating variables. Dimensionality techniques used in the analysis are Principal Component Analysis (PCA), Factor Analysis (FA), Canonical Correlation Analysis (CCA)
- Host: GitHub
- URL: https://github.com/tatevkaren/multivariate-statistics
- Owner: TatevKaren
- Created: 2021-02-07T11:10:20.000Z (almost 4 years ago)
- Default Branch: main
- Last Pushed: 2021-02-27T13:44:17.000Z (almost 4 years ago)
- Last Synced: 2023-10-20T23:20:39.688Z (about 1 year ago)
- Topics: canonical-correlation-analysis, dimensionality-reduction, factor-analysis, multivariate-analysis, multivariate-statistics, principal-component-analysis
- Language: R
- Homepage:
- Size: 800 KB
- Stars: 7
- Watchers: 1
- Forks: 2
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# Case Study in Ranking US Cities
**Paper:** MultivariateStatistics_CaseStudy_PCA_FA_CCA.pdf
**Code:** MultivariateStat_PCA_FA_CCA_code.R
Case Study in ranking U.S. cities based on a single linear combination of rating variables. Dimensionality techniques used in the analysis are Principal Component Analysis (PCA), Factor Analysis (FA), Canonical Correlation Analysis (CCA).
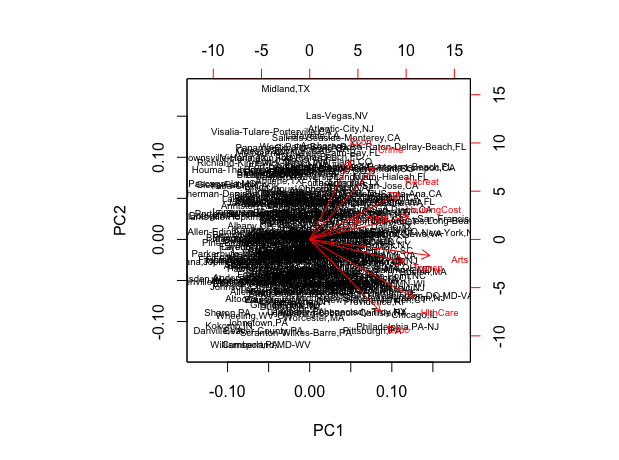
**Principal Component Analysis (PCA) Screenshots**
Biplot with scaled data where yoou can observe that Crime and Education have the smallest margins and the remaining variables show substantial variations. First three principal components explain 63.10% of the total variation in data. Applying the ”elbow rule” it can be seen that one can optimally retain 3 components.
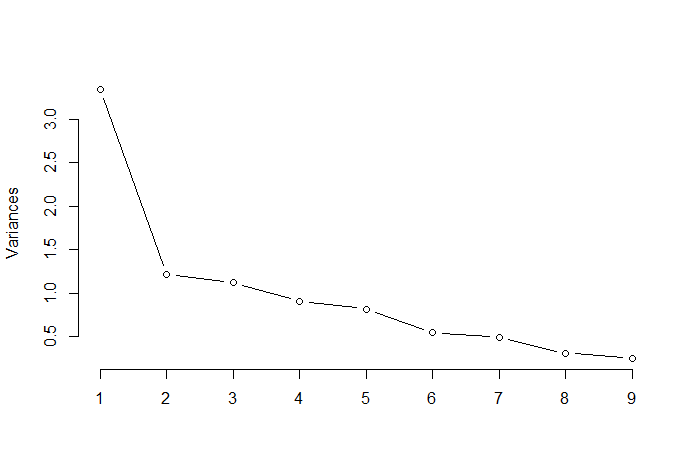
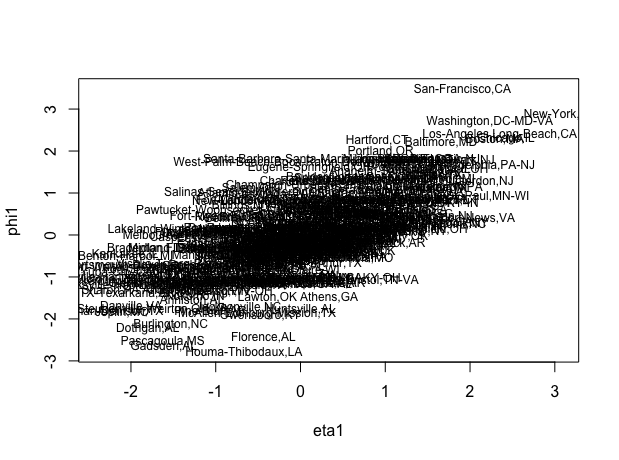
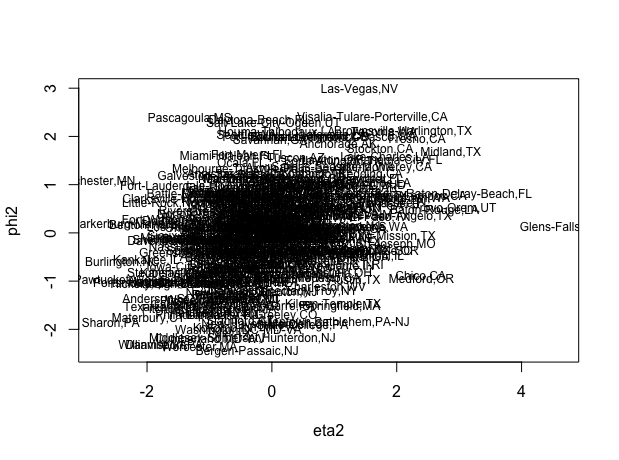
**Canonical Correlation Analysis (CCA) Screenshots**
Figures showing clear correlation between X and Y scores for the first canonical correlation which is not the case for the second factor, where one can observe some correlation but not significant. This shows that the first canonical correlation is important but second one is not.
