https://github.com/thomasafink/orbital-mechanics
A comprehensive 3D visualization of our solar system including planets, moons, asteroid belts, and the Oort cloud implemented in Python using Matplotlib.
https://github.com/thomasafink/orbital-mechanics
asteroid-belt asteroids astro astrophysics nasa orbital-dynamics orbital-mechanics orbits physics python simulation solar solar-system space system
Last synced: 8 months ago
JSON representation
A comprehensive 3D visualization of our solar system including planets, moons, asteroid belts, and the Oort cloud implemented in Python using Matplotlib.
- Host: GitHub
- URL: https://github.com/thomasafink/orbital-mechanics
- Owner: ThomasAFink
- License: mit
- Created: 2024-11-26T19:16:03.000Z (about 1 year ago)
- Default Branch: main
- Last Pushed: 2025-01-19T15:27:30.000Z (11 months ago)
- Last Synced: 2025-01-28T19:20:31.292Z (10 months ago)
- Topics: asteroid-belt, asteroids, astro, astrophysics, nasa, orbital-dynamics, orbital-mechanics, orbits, physics, python, simulation, solar, solar-system, space, system
- Language: Python
- Homepage:
- Size: 60.5 KB
- Stars: 1
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# Solar System 3D Animation
A comprehensive 3D visualization of our solar system including planets, moons, asteroid belts, and the Oort cloud implemented in Python using Matplotlib.

## Features
- Full 3D representation of the solar system
- Accurate orbital mechanics based on Kepler's laws
- Includes all planets and major moons
- Visualization of:
- Asteroid Belt
- Hildas Group
- Jupiter Trojans
- Kuiper Belt
- Inner Oort Cloud (Hills Cloud)
- Outer Oort Cloud
- Dynamic camera with smooth zoom
- Multiple output formats (GIF, 1080p MP4, 4K MOV)
- Light and dark theme options
## Mathematical Physics
### Orbital Mechanics
The simulation uses Kepler's laws of planetary motion to calculate orbital positions:
1. **Kepler's First Law**: Orbits are elliptical with the Sun at one focus
}{1+e\cos\theta})
where:
- r = distance from the sun
- a = semi-major axis
- e = eccentricity
- θ = true anomaly
2. **Kepler's Second Law**: Equal areas are swept in equal times
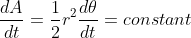
3. **Kepler's Third Law**: The square of the orbital period is proportional to the cube of the semi-major axis
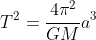
### 3D Position Calculation
The position of celestial bodies is calculated using:
```mermaid
graph TD
A[Orbital Elements] --> B[Calculate in Orbital Plane]
B --> C[Apply Inclination]
C --> D[Apply Ascending Node]
D --> E[Final 3D Position]
```
Position calculation formula:
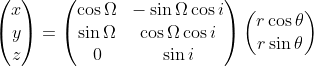
Where:
- Ω = ascending node
- i = inclination
- r = orbital radius
- θ = orbital angle
## System Architecture
```mermaid
classDiagram
class Config {
+SETTINGS: dict
+frames: int
+camera_distance: float
+planets: dict
+asteroid_counts: dict
}
class SolarSystemAnimation3D {
+init_positions()
+update(frame)
+calculate_3d_position()
+calculate_visibility()
+animate()
+save()
+save1080p()
+save4k()
}
Config -- SolarSystemAnimation3D
```
## Requirements
- Python 3.7+
- NumPy
- Matplotlib
- FFmpeg (for video output)
## Installation
```bash
pip install numpy matplotlib
# For video output
apt-get install ffmpeg # Linux
brew install ffmpeg # macOS
```
## Usage
Basic usage:
```python
from complete_solar_system_3d import SolarSystemAnimation3D
# Create animation
solar_system = SolarSystemAnimation3D(style='default')
# Display animation
solar_system.animate()
# Save as GIF
solar_system.save("solar_system.gif")
# Save as 1080p video
solar_system.save1080p("solar_system_1080p.mp4")
# Save as 4K video
solar_system.save4k("solar_system_4k.mov")
```
## Customization
You can modify the Config.SETTINGS dictionary to:
- Adjust animation frames
- Change camera behavior
- Modify planet/moon properties
- Adjust asteroid population sizes
## Performance Notes
- The animation is computationally intensive, especially with large asteroid populations
- 4K rendering requires significant memory and processing power
- Consider reducing asteroid counts for smoother performance
## License
MIT License - feel free to use and modify for your own projects!