https://github.com/timothymakkison/graham_convex_hull

Implementation of the Graham scan method to find the convex hull of a series of points in rust. For use in https://github.com/TimothyMakkison/transportation_network.
https://github.com/timothymakkison/graham_convex_hull

algorithm convex-hull rust rust-lang

Last synced: 9 months ago
JSON representation

Implementation of the Graham scan method to find the convex hull of a series of points in rust. For use in https://github.com/TimothyMakkison/transportation_network.

• Host: GitHub
• URL: https://github.com/timothymakkison/graham_convex_hull
• Owner: TimothyMakkison
• Created: 2021-08-22T22:52:53.000Z (over 4 years ago)
• Default Branch: master
• Last Pushed: 2021-09-23T21:41:24.000Z (about 4 years ago)
• Last Synced: 2025-01-21T02:12:38.757Z (11 months ago)
• Topics: algorithm, convex-hull, rust, rust-lang
• Language: Rust
• Homepage:
• Size: 7.81 KB
• Stars: 0
• Watchers: 1
• Forks: 0
• Open Issues: 0
• Metadata Files:
  • Readme: README.md

Awesome Lists containing this project

README

          
# graham_convex_hull

Implementation of the Graham scan method to find the convex hull of a series of points in rust. For use in my graph [transportation network](https://github.com/TimothyMakkison/transportation_network) problem to find the two points with the greatest distance in O(nlog(n)) time. 

## Convex hull

A convex hull of a shape is defined as the smallest number of points required to enclose the remaining points. 

The convex hull has many applications in Maths, Statistics, Physics and Computer science.

![Image](https://miro.medium.com/max/677/1*F4IUmOJbbLMJiTgHxpoc7Q.png)

![Cow Image](https://www.wolfram.com/mathematica/new-in-10/data-and-mesh-regions/HTMLImages.en/convex-hulls/O_12.png)

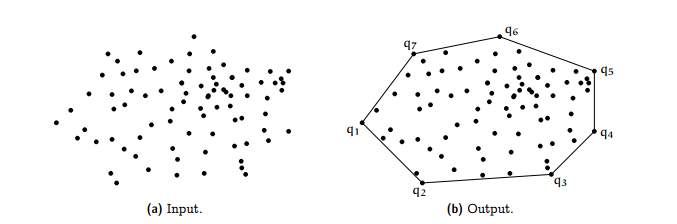
## Graham scan algorithm

Graham scan algorithm finds the convex hull of a series of points in O(n log(n)) time. It does so by calculating the angle between every point and the lowest point, 

and then sorting in ascending order. The sorted algorithms are iterated through with three points at a time being tested for whether they for a clockwise or anti clockwise angle.

## Pseudocode

```

Assuming the input length is greater than 3.

1. Find the lowest / furthest left point -> min.

2. Calculate the angle between each point and min using atan2().

3. Sort the points by angle in ascending order -> sorted.

4. Take the first two values from sorted and add them to a stack.

5. Foreach remaining value from sorted: 

6.      Take top two values from stack and point. 

7.      Calculate if the three points make a clockwise of counter clockwise turn.

8.      If clockwise pop stack and recalculate turn, repeating step 7.

9.      If anti clockwise add point to stack

10. Return stack.

```