https://github.com/tomekzaw/ewl
A Python tool for symbolic analysis of quantum games in EWL protocol with IBM Q integration.
https://github.com/tomekzaw/ewl
ewl ibmq python qiskit quantum sympy
Last synced: 4 months ago
JSON representation
A Python tool for symbolic analysis of quantum games in EWL protocol with IBM Q integration.
- Host: GitHub
- URL: https://github.com/tomekzaw/ewl
- Owner: tomekzaw
- License: mit
- Created: 2021-04-19T20:38:24.000Z (over 4 years ago)
- Default Branch: master
- Last Pushed: 2022-05-07T19:55:48.000Z (over 3 years ago)
- Last Synced: 2025-07-08T06:06:15.356Z (4 months ago)
- Topics: ewl, ibmq, python, qiskit, quantum, sympy
- Language: Python
- Homepage: https://pypi.org/project/ewl/
- Size: 3.71 MB
- Stars: 9
- Watchers: 1
- Forks: 1
- Open Issues: 3
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# EWL
A simple Python library to simulate and execute EWL quantum circuits on IBM Q with symbolic calculations using SymPy.
## Installation
```bash
pip install ewl
```
## Examples
- Prisoner's dilemma
- [Two players](https://github.com/tomekzaw/ewl/blob/master/examples/example.ipynb)
- [Three players](https://github.com/tomekzaw/ewl/blob/master/examples/three_players.ipynb)
- [Payoff function 3D plot](https://github.com/tomekzaw/ewl/blob/master/examples/payoff_function_plot_3d.ipynb)
- [Simulation with predefined gate noises](https://github.com/tomekzaw/ewl/blob/master/examples/noise_model.ipynb)
## Usage
### Initialization
This library uses [SymPy](https://www.sympy.org/en/index.html) to perform symbolic calculations. It's convenient to import it as `sp` and define frequently used constants for future use.
```python
import sympy as sp
i = sp.I
pi = sp.pi
sqrt2 = sp.sqrt(2)
```
When using this library in Jupyter Notebook, call [`init_printing`](https://docs.sympy.org/latest/tutorial/printing.html#setting-up-pretty-printing) to enable pretty printing.
```python
sp.init_printing()
```
### EWL instance
First, you need to define the initial (preferably entangled) quantum state:
```python
from sympy.physics.quantum.qubit import Qubit
psi = (Qubit('00') + i * Qubit('11')) / sqrt2
```
It is also necessary to define two unitary strategies that represent the classical strategies:
```python
C = sp.Matrix([
[1, 0],
[0, 1],
])
D = sp.Matrix([
[0, i],
[i, 0],
])
```
Then you need to define the players' strategies. Each strategy must be a unitary matrix as it represents a single-qubit quantum gate.
```python
alice = sp.Matrix([
[1, 0],
[0, 1],
])
```
The library comes with a series of built-in parametrizations, including the original one from EWL paper as well as other 2- and 3 degrees of freedom parametrizations (see [here](https://github.com/tomekzaw/ewl/blob/master/src/ewl/parametrizations.py)).
```python
from ewl.parametrizations import *
bob = U_Eisert_Wilkens_Lewenstein(theta=pi / 2, phi=0)
```
At this point you can also use arbitrary symbols and compound expressions to generalize the analysis.
```python
theta, gamma = sp.symbols('theta gamma', real=True)
charlie = U_Eisert_Wilkens_Lewenstein(theta=theta, phi=gamma / 2)
```
You also need to define the payoff matrix, possibly with symbols, for arbitrary number of players.
```python
payoff_matrix = sp.Array([
[
[3, 0],
[5, 1],
],
[
[3, 5],
[0, 1],
],
])
```
Finally, you can make an instance of quantum game in the EWL protocol by providing the initial quantum state, a list of players' strategies and the payoff matrix with corresponding shape. The library supports arbitrary number of players, although it works best for 2-player games.
```python
from ewl import EWL
ewl = EWL(psi=psi, C=C, D=D, players=[alice, bob], payoff_matrix=payoff_matrix)
```
### Calculations
Based on the provided initial quantum state, the library automatically calculates the corresponding matrix of *J* and *J*† gates.
```python
ewl.J
ewl.J_H
```
Based on the players' strategies, the library also calculates the amplitudes of the result quantum state in the computational basis.
```python
ewl.amplitudes()
ewl.amplitudes(simplify=False)
```
From the amplitudes one can easily derive the probabilities of possible game results. By default, the expressions are simplified using trigonometric identities. Make sure to enable `real=True` flag when defining real-valued symbols to allow for further simplification.
```python
ewl.probs()
ewl.probs(simplify=False)
```
Finally, based on the payoff matrix and previously mentioned probabilities, the library calculates the payoff functions as symbolic expressions (possibly with parameters from the initial state and strategies).
```python
ewl.payoff_function(player=0) # first player
ewl.payoff_function(player=1, simplify=False) # second player
ewl.payoff_function(player=None) # payoff sum
```
You can also obtain a tuple containing the payoffs for each respective player.
```python
ewl.payoffs()
ewl.payoffs(simplify=False)
```
For quantum games parametrized with exactly two symbols, it is possible to plot a three-dimensional graph of the payoff function.
```python
from ewl.plotting import plot_payoff_function
plot_payoff_function(
ewl, player=0,
x=alpha, x_min=0, x_max=pi / 2,
y=beta, y_min=0, y_max=pi / 2)
```
### Parameters
Here's how you can list all symbols used either in the initial quantum state or in the players' strategies:
```python
ewl.params
```
You can also substitute the symbols with specific values to obtain a non-parametrized instance of quantum game as new EWL instance:
```python
ewl_fixed = ewl.fix(theta=0, gamma=pi / 2)
```
It is also possible to substitute specific players' strategies for further analysis of a certain case of the game.
```python
ewl_CD = ewl.play(C, D)
```
### Mixed strategies
The library also supports quantum games with mixed strategies. You can define a mixed strategy by passing a list of probabilities and corresponding pure strategies:
```python
from ewl.mixed import MixedStrategy
alice = MixedStrategy([(p1, U1), (p2, U2)])
```
**Note:** The library will check if the probabilities sum up to 1. To disable this check, pass `check_sum=False`.
Then you can create an instance of EWL quantum game with mixed strategies:
```python
from ewl.mixed import MixedEWL
mixed_ewl = MixedEWL(psi=psi, C=C, D=D, players=[alice, bob], payoff_matrix=payoff_matrix)
```
The major difference is that you cannot call `amplitudes` method due to the fact that the state of quantum game with mixed strategies cannot be expressed as a vector in a general case. Instead, you can calculate the density matrix.
```python
mixed_ewl.density_matrix()
```
Other properties and methods such as `J`, `J_H`, `params`, `fix`, `probs` and `payoff_function` behave similarly as for the regular EWL instance with pure strategies.
### Example games
The library comes with a series of built-in example games, in particular a few variants of Quantum Prisoner's Dilemma with different parametrizations from various articles (see [here](https://github.com/tomekzaw/ewl/blob/master/src/ewl/games.py)).
### Qiskit integration
This library also integrates with [Qiskit](https://qiskit.org/), allowing arbitrary quantum games in the EWL protocol to be executed on [IBM Q](https://www.ibm.com/quantum-computing/) devices. First, you need to load your credentials:
```python
from qiskit import IBMQ
IBMQ.load_account()
```
When running locally, make sure to save the access token to disk first using [`IBMQ.save_account`](https://qiskit.org/documentation/stubs/qiskit.providers.ibmq.IBMQFactory.save_account.html).
In order to access backend-specific features of EWL instance, first you need to convert it to `EWL_IBMQ` instance. Note that the input quantum game must be non-parametrized (cannot have any symbols).
```python
from ewl.ibmq import EWL_IBMQ
ewl_ibmq = EWL_IBMQ(ewl_fixed)
```
You can also specify and apply noise model used in quantum simulation.
```python
from qiskit.providers.aer.noise import NoiseModel, pauli_error
p_error = 0.05
bit_flip = pauli_error([('X', p_error), ('I', 1 - p_error)])
phase_flip = pauli_error([('Z', p_error), ('I', 1 - p_error)])
noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(bit_flip, ['u1', 'u2', 'u3'])
noise_model.add_all_qubit_quantum_error(phase_flip, ['x'], [0])
ewl_ibmq = EWL_IBMQ(ewl_fixed, noise_model=noise_model)
```
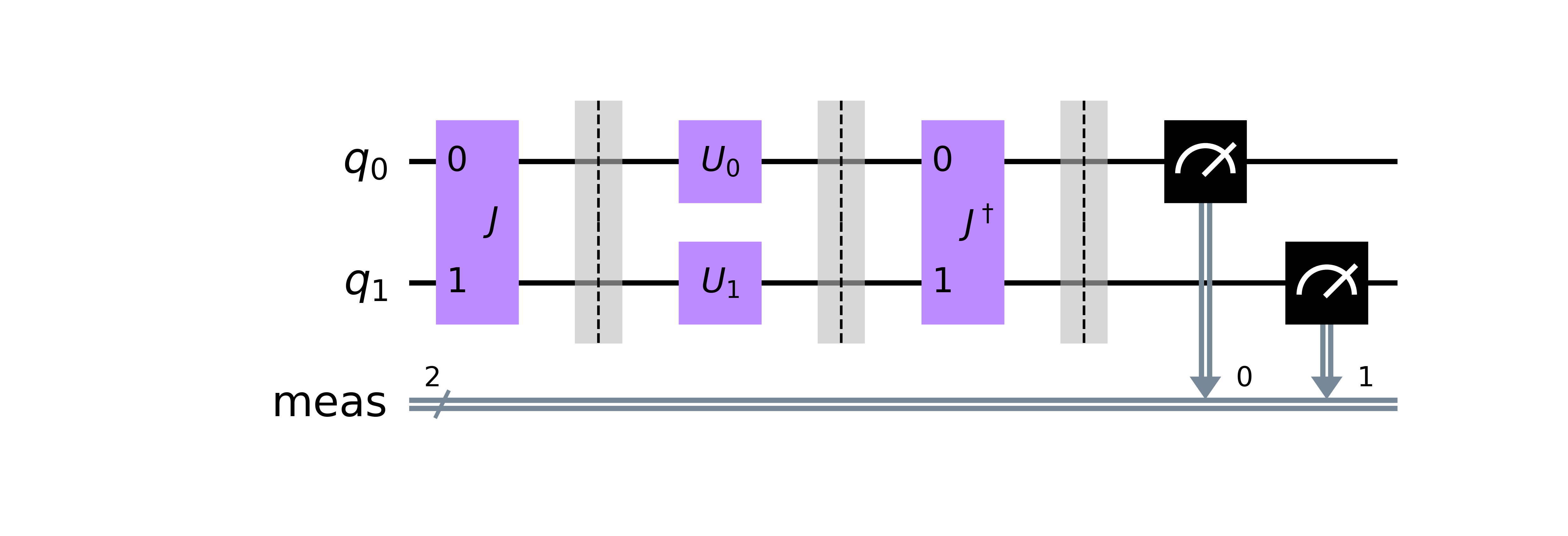
You can draw the original quantum circuit of quantum game in the EWL protocol.
```python
ewl_ibmq.draw()
```
It is also possible to draw the quantum circuit transpiled for a specific backend.
```python
ewl_ibmq.draw_transpiled(backend_name='ibmq_quito', optimization_level=3)
```
Here's how you can execute the quantum game on a specific statevector simulator:
```python
ewl_ibmq.simulate_probs(backend_name='statevector_simulator')
```
You may also run the quantum circuit on QASM simulator and get histogram data of the experiment.
```python
ewl_ibmq.simulate_counts(backend_name='qasm_simulator')
```
Finally, you can run the quantum game on a real quantum device:
```python
ewl_ibmq.run(backend_name='ibmq_quito', optimization_level=3)
```
## Citation
```bibtex
@software{PythonEWL2022,
author = {Tomasz Zawadzki and Piotr Kotara},
title = {A Python tool for symbolic analysis of quantum games in EWL protocol with IBM Q integration},
howpublished = {\url{https://github.com/tomekzaw/ewl}},
}
```