https://github.com/tonitaga/graph-algorithms-cpp-console
Basic algorithms on graphs: BFS, DFS, Dijkstra Algorithm, Floyd-Worshell Algorithm, Prima Algorithm, Ant Algorithm in C++ programming language
https://github.com/tonitaga/graph-algorithms-cpp-console
algorithms article cpp
Last synced: 5 months ago
JSON representation
Basic algorithms on graphs: BFS, DFS, Dijkstra Algorithm, Floyd-Worshell Algorithm, Prima Algorithm, Ant Algorithm in C++ programming language
- Host: GitHub
- URL: https://github.com/tonitaga/graph-algorithms-cpp-console
- Owner: tonitaga
- License: unlicense
- Created: 2023-08-02T19:20:50.000Z (almost 2 years ago)
- Default Branch: main
- Last Pushed: 2023-08-27T20:13:51.000Z (almost 2 years ago)
- Last Synced: 2024-11-09T06:07:12.650Z (7 months ago)
- Topics: algorithms, article, cpp
- Language: C++
- Homepage: https://habr.com/ru/companies/timeweb/articles/751762/
- Size: 179 KB
- Stars: 3
- Watchers: 1
- Forks: 1
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
> Всем привет! Меня зовут **Нурислам (aka tonitaga)**,и сегодня я бы вам хотел рассказать об **Базовых алгоритмах на графах**.
## Что такое граф?
- Я не стану подробно описывать, что такое граф, так как полно других источников, но скажу, что задача из ОГЭ(ЕГЭ) по информатике на нахождение кратчайшего пути, это и есть граф.
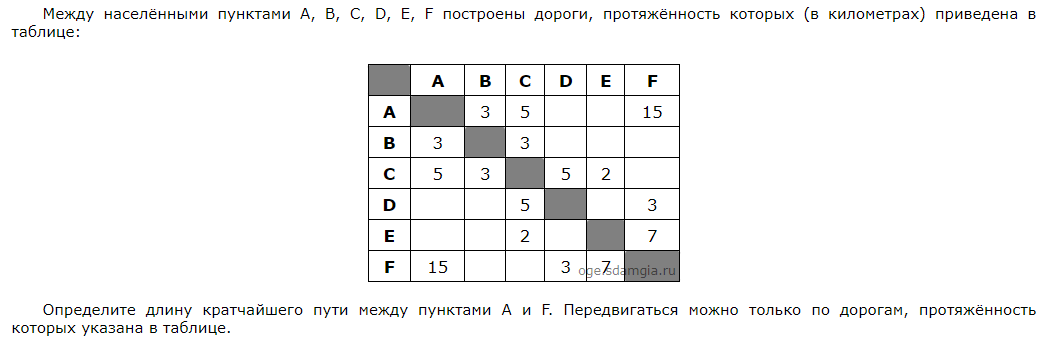
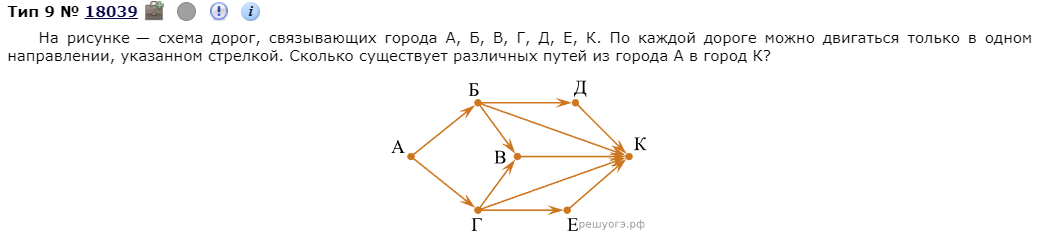
- Держите ссылочку на основную информацию о графах: [Графы](https://ru.wikipedia.org/wiki/Граф_(математика))
- Больше про терминологию в мире графов можно прочитать [здесь](https://www.techiedelight.com/ru/terminology-and-representations-of-graphs/)
## Рассматриваемые алгоритмы
- Обход графа в ширину (Поиск в ширину) aka BFS | **Breadth First Search**
- Обход графа в глубину (Поиск в глубину) aka DFS | **Depth First Search**
- **Алгоритм Дейкстры**
- **Алгоритм Флойда-Уоршелла**
- **Алгоритм Прима**
## Причина написания статьи
- **Объединение** базовых алгоритмов на графах в одну статью (понятно, что для каждого базовые алгоритмы на графах это свое, но я выделил те, которые сам считаю базовыми)
## Представление графа в коде
- Представим граф в виде класса обёртки над [матрицей смежности](https://ru.wikipedia.org/wiki/Матрица_смежности). Класс-wrapper будет знать количество рёбер, вершин, и тип графа. Обычно такого функционала хватает для большинства алгоритмов.
---
## BFS & DFS
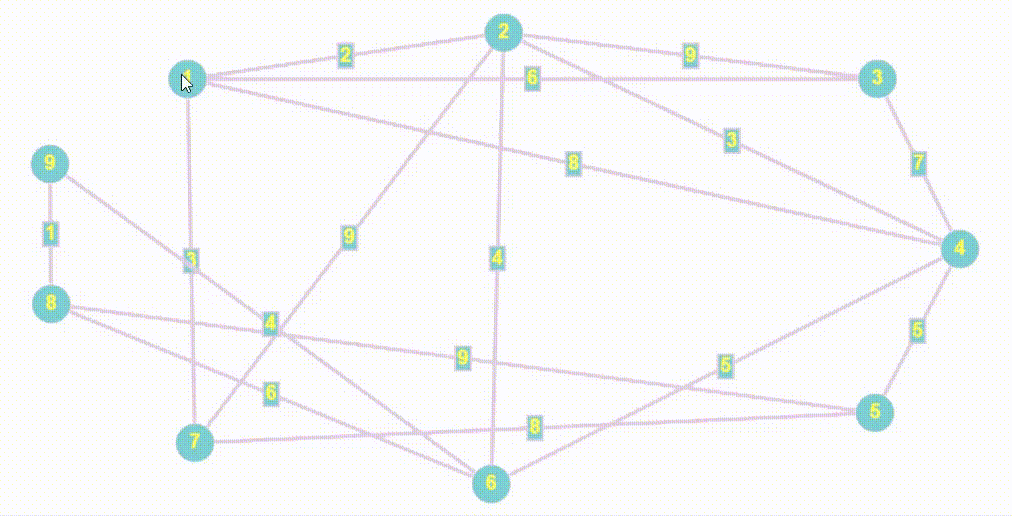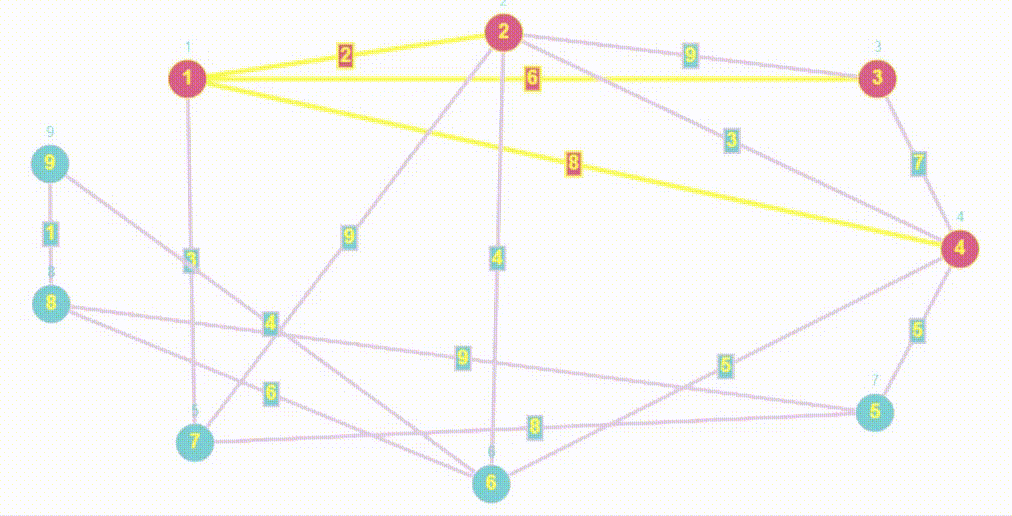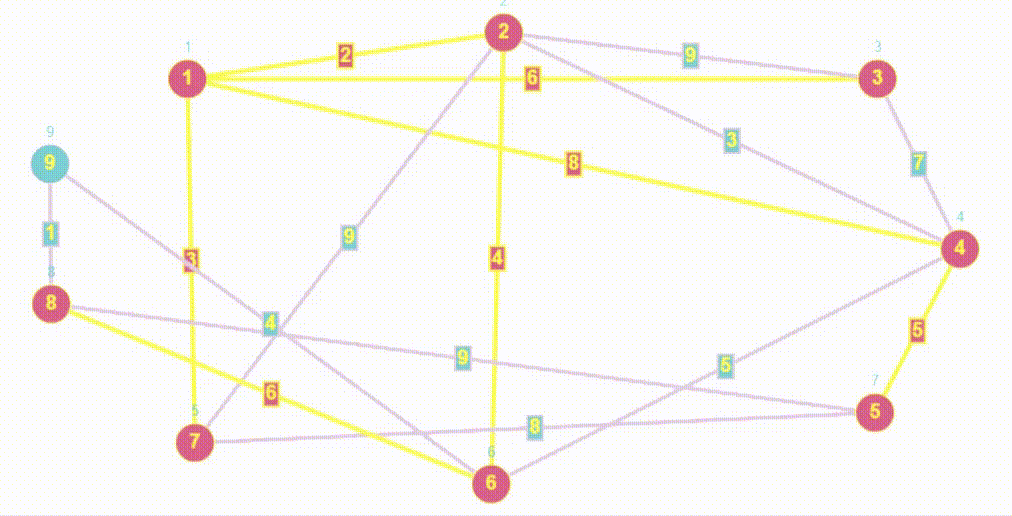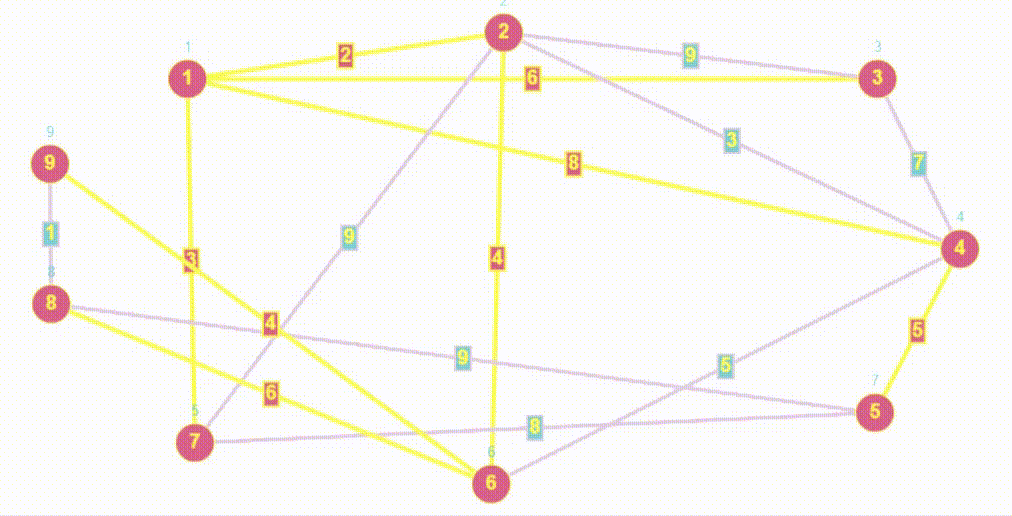
- BFS (breadth first search) - это алгоритм, используемый для обхода или поиска в графах и деревьях. Он начинается с выбранной вершины и обходит сначала все доступные вершины на текущем уровне перед переходом на следующий уровень.
- Алгоритм BFS очень похож на [Волновой алгоритм](https://habr.com/ru/articles/745294/), так как волновой алгоритм относится к семейству алгоритмов основанных на методах поиска в ширину.
- Обход в ширину работает на основе очереди
- **Сложность алгоритма обхода в ширину** является линейной и равна **O(V+E)**, где V - количество вершин графа, E - количество ребер в графе.
## Алгоритм
1. На вход в функцию BFS приходит граф и стартовая вершина
2. Возвращать BFS будет массив порядка посещения вершин (пометим как **enter_order**)
3. Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
4. Кладем в очередь нашу стартовую вершину и кладем в **enter_order** нашу стартовую вершину
5. Пока наша очередь
5.1. Получаем элемент из очереди (пометим это как **from**) (в очереди хранится лишь порядковый номер вершины)
5.2. Удаляем вытащенный элемент из очереди
5.3. Перебирая все вершины графа:
5.3.1. Если перебираемая вершина (пометим как **to**) непосещенная и по матрице смежности между **from и to** есть ребро, то
5.3.1.1. Помечает вершину **to** как посещенную
5.3.1.2. Кладем эту вершину в очередь и **enter_order**
5.3.2. Иначе ничего не делаем
6. Возвращаем **enter_order**
---

- DFS (depth first search) - это алгоритм, используемый для обхода или поиска в графах и деревьях. Он начинается с выбранной вершины и обходит все доступные вершины на максимальную глубину, прежде чем возвращаться к следующей непосещенной вершине.
- Основное отличие BFS от DFS только в том, что **BFS используется очередь** а **DFS используется stack**, в остальном алгоритм обхода практически не отличается
- Обычно все реализовывают рекурсивный обход в глубину, я распишу алгоритм итеративного обхода в глубину
- **Сложность алгоритма обхода в глубину** такая же как и у BFS алгоритма, и равна **O(V+E)**, где V - количество вершин графа, E - количество ребер в графе.
## Алгоритм
1. На вход в функция DFS приходит граф и стартовая вершина
2. Возвращать BFS будет массив порядка посещения вершин (пометим как **enter_order**)
3. Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
4. Кладем в стек нашу стартовую вершину и кладем в **enter_order** нашу стартовую вершину
5. Пока наш стек не пустой:
5.1. Получаем элемент из стека (пометим это как **from**)
5.2. Перебирая все вершины графа:
5.2.1. Если перебираемая вершина (пометим как **to**) непосещенная и по матрице смежности между **from и to** есть ребро, то
5.2.1.1. Помечаем вершину to как посещенную
5.2.1.2. Кладем эту вершину в стек и в **enter_order**
5.2.1.3. Присваиваем вершине **from** значение вершины **to** (Это нужно для того чтобы просматривать ребра в глубину)
5.2.2. Иначе ничего не делаем
5.3. Если условие 5.2.1 не выполнилось выполнилось, то удаляем из стека наш верхний элемент
6. Возвращаем **enter_order**
---
## Алгоритм Дейкстры
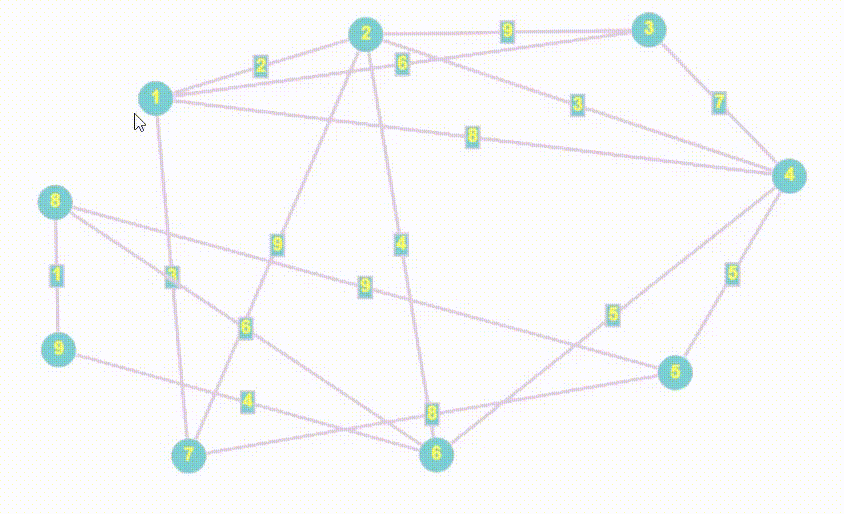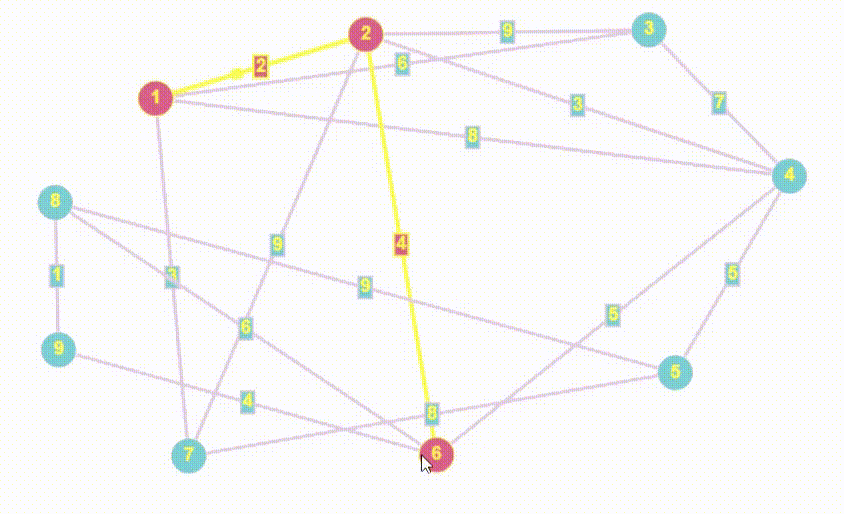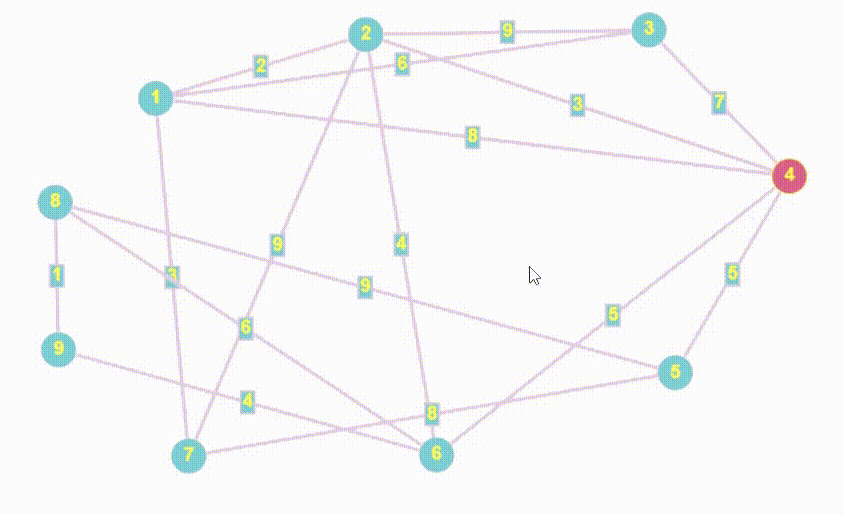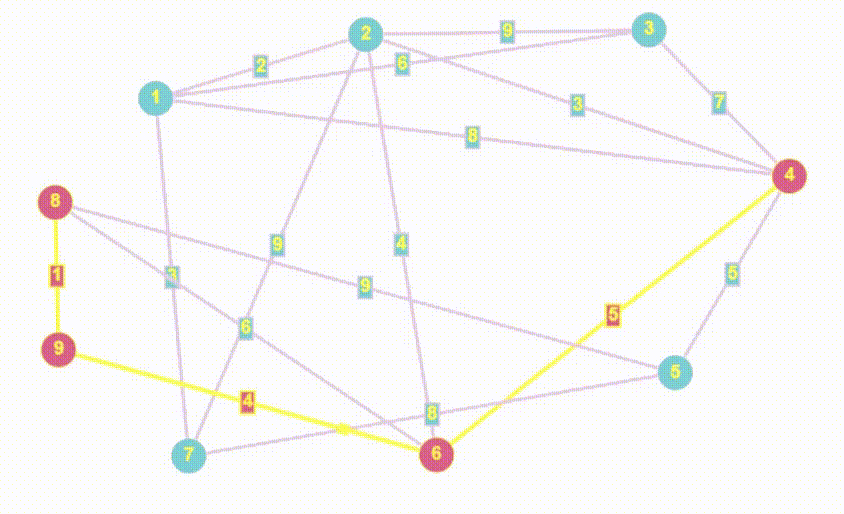
- Алгоритм Дейкстры - это алгоритм нахождения кратчайшего пути от одной вершины графа до всех остальных вершин. Он работает только с неотрицательными весами ребер и является одним из самых эффективных алгоритмов для нахождения кратчайших путей в графах.
- Алгоритм Дейкстры принципом работы очень похож на BFS
- Полный алгоритм Дейкстры возвращает массив кратчайших расстояний от стартовой точки до всех остальных, мы найдем все расстояния, но вернем лишь то, которое хочет пользователь
- Единственным минусом алгоритма Дейкстры являемся, неумение работать с отрицательными весами ребер
- **Сложность Алгоритма Дейкстры** растет линейно-логарифмически и равна **O(ЕlogV)**, где V - количество вершин графа, E - количество ребер графа. Такая сложность делает его эффективным при работе с большими графами.
- Основным применением является нахождение кратчайшего пути между двумя вершинами графа. Он может быть использован в сетевых задачах, таких как определение оптимального пути для передачи данных по сети или для оптимизации маршрутов в GPS-навигации.
## Алгоритм
1. На вход функция Алгоритма Дейкстры будет принимать граф и две вершины, стартовая (пометим как **start**) и конечная (пометим как **finish**)
2. Создадим массив длин от **start** до всех остальных вершин (пометим как **distance**), изначально пометим все длины в массиве бесконечностью.
3. Стартовую точку в **distance** пометим как 0, потому что расстояние от точки, до самой точки равно нулю (в данном алгоритме мы не рассматриваем ситуации когда есть петли)
4. Создаем множество из пары значений, пара будет хранить длину и индекс вершины
5. Инициализируем наше множество стартовым значением, за стартовое значение отвечает стартовая вершина, поэтому в множестве будет лежать: длина -> 0 и индекс **start**
6. Пока наше множество не пусто:
6.1. Получаем начальный элемент в множестве (пометим как **from**) (вспоминаем, что в множестве хранится пара значений, нам нужен лишь индекс вершины)
6.2. Удаляем начальный элемент из множества
6.3. Перебирая все вершины графа:
6.3.1. Если между from и перебираемой вершиной (пометим как **to**) есть ребро
6.3.2. И если расстояние от **start до to** больше чем расстояние от **start до from** + вес самого ребра (**from, to**)
6.3.2.1. Удаляем из множества старую пару значений: **{расстояние от start до to, индекс вершины to}**
6.3.2.2. В distance обновляем расстояние от **start до to** на более короткое, которое мы проверяли в условии 6.3.2
6.3.2.3. Вставляем в множество обновленную пару: **{расстояние от start до to, индекс вершины to}**
7. Возвращаем из массива** distance** расстояние под индексом **finish**
---
## Алгоритм Флойда-Уоршелла

- Алгоритм Флойда-Уоршелла - это алгоритм поиска кратчайших путей во [взвешенном](https://ru.hexlet.io/courses/graphs/lessons/minimum_spanning/theory_unit) и не взвешенном графе с положительным или отрицательным весом ребер (но без отрицательных циклов). За одно выполнение алгоритма будут найдены длины (суммарные веса) кратчайших путей между всеми парами вершин.
- Логично что алгоритм будет возвращать матрицу расстояний между всеми парами вершин (грубо говоря новую матрицу смежности)
- Алгоритм не содержит детали о самих кратчайших путях, а запоминает лишь кратчайшее расстояние, но алгоритм можно усовершенствовать, ссылка на видео [здесь](https://www.youtube.com/watch?v=8JQ565Rz7d8&t=04m20s), да и описание вместе с реализацией можно посмотреть там же.
- **Сложность Алгоритма Флойда-Уоршелла** независимо от типа графа **O(V^3)**, где V - количество вершин.
- Можно сказать что алгоритм Флойда-Уоршелла делает тоже самое, что и алгоритм Дейкстры, только находит кратчайшие расстояния не только между двумя вершинами, а всеми сразу.
## Алгоритм
1. На вход функция Алгоритма Флойда-Уоршелла будет принимать только сам граф
2. Создаем копию матрицы смежности графа (пометим как **distance**)
2.1. Основное отличие **distance** от той, которая лежит в графе лишь в том, что все нули в матрице смежности графа, в матрице distance будут бесконечностью (кроме главной диагонали), так как главная диагональ хранит в себе расстояние от вершины до самой себя, поэтому и ноль (мы не учитываем ситуации с петлями, предположим что их нет)
3. Постепенно открывая доступ к вершинам (открытие доступа к вершине означает, что мы просто перебираем все вершины с индексами от 0 до V - 1 (конечно же, если индексация нулевая)), пусть вершина, к которой открыли доступ называется **v**:
3.1. Просматривая все возможные и невозможные ребра в графе (в двух циклах пробегаемся по матрице **distance**), пусть счетчик внешнего цикла будет называться **row**, а счетчик вложенного цикла будет называться** col**:
3.1.1. Получаем суммарный вес ребер **{row, v} и {v, col}**
3.1.2. Если ребро **{row, v}** и ребро **{v, col}** существуют и текущее значение в матрице **distance** под индексами **{row, col}** больше чем суммарный вес двух новых ребер, то:
3.1.2.1. Обновляем в матрице **distance** расстояние на более короткое, которое мы вычислили в пункте 3.1.1
3.1.3. Иначе ничего не делаем
4. Возвращаем матрицу **distance**

---
## Алгоритм Прима
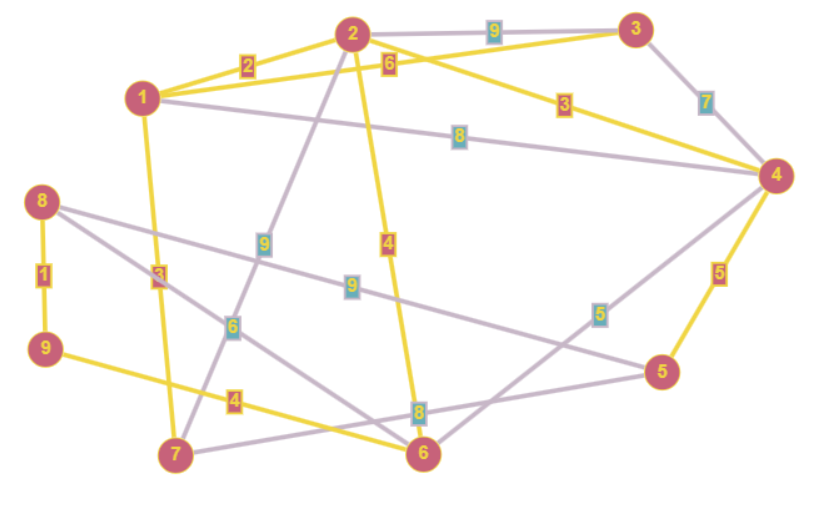
- Алгоритм Прима - это алгоритм нахождения [минимального остовного дерева](https://ru.wikipedia.org/wiki/Минимальное_остовное_дерево) (MST) в связном взвешенном графе. Он начинает с выбранной стартовой вершины и постепенно добавляет ребра с наименьшим весом, чтобы связать все вершины графа.
- Алгоритм Прима работает с [неориентированными графами](https://www.geeksforgeeks.org/what-is-unidrected-graph-undirected-graph-meaning/), поэтому если нам был передам ориентированный граф, мы будем игнорировать направление ребер.
- **Сложность Алгоритма Прима** растет логарифмически и равна **O(ElogV)**, где V - количество вершин графа, E - количество ребер в графе.
- Остовное дерево должно включать в себя все вершины графа
- Каждая вершина должна быть посещена ровно 1 раз
- Результатом работы Алгоритма прима будет матрица смежности дерева
> Скажу сразу, что моя реализация не умеет работать с графами у которых, есть изолированные вершины, как только я это сделаю я изменю статью, спасибо за понимание.
## Алгоритм
1. Создаем два множеств, для посещенных и не посещенных вершин (пометим, соответственно, как **visited и unvisited**)
2. Создаем исходную матрицу, которая будет представлять собой остовное дерево (пометим как **spanning_tree**)
3. Создаем массив ребер (пометим как **tree_edges**), ребро в данном случае это структура, которая хранит две вершины и вес самого ребра.
4. Инициализируем множество непосещенных вершин всеми, существующими в графе вершинами
5. Выбираем, случайным образом, вершину, от которой будет строиться остовное дерево, и помечаем эту вершину как посещенной, соответственно из множества непосещенных ее убираем
6. Пока множество непосещенных першин не пусто:
6.1. Создаем ребро инициализируя его поля бесконечностями
6.2. Перебирая все посещенные вершины (пометим как **from**):
6.2.1. Перебираем все вершины графа (пометим как **to**):
6.2.1.1. Если to является непосещенной вершиной и ребро между вершинами **{from, to}** существует и вес ребра (созданного в пункте 5.1) больше чем вес ребра между вершинами **{from, to}**, то:
6.2.1.1.1. Обновляем ребро (5.1) вершинами **from и to** и весом между этими вершинами
6.3. Если вес ребра не равен бесконечности:
6.3.1. Добавляем в массив **tree_edges** новое ребро
6.3.2. Удаляем из множества непосещенных вершин вершину **to**
6.3.3. Добавляем в множество посещенных вершин вершину **to**
6.3.4. Иначе прекращаем цикл
7. Пробегаясь по всем ребрам массива **tree_edges**:
7.1. Инициализируем **spanning_tree**, добавляя в нее ребра (добавлять нужно в обе стороны, чтобы граф получился неориентированным)
8. Возвращаем **spanning_tree**
---
## Для чего используют эти алгоритмы?
## BFS
- Алгоритм BFS используется для решения задач поиска оптимального пути. Одной из таких задач считается поиск выхода из лабиринта.
- Для задач искусственного интеллекта, связанных с поиском решения с минимальным количеством ходов. В таком случае состояния «умной машины» представляются как вершины, а переходы между ними — как ребра.
- Конечно, еще не мало примеров, где используется BFS, но я привел пару примеров.
## DFS
- Также как и алгоритм BFS, DFS может быть использован для нахождения пути в лабиринте, однако DFS используется для поиска произвольного маршрута в лабиринте. BFS ищет оптимальный путь в лабиринте, а DFS ищет не всегда самый короткий (исключая ситуации, когда в лабиринте между двумя точками единственный путь).
- Пример использования DFS вне программирования: Правило прохождения лабиринта, придерживаясь правила левой руки, ну либо правой руки.
- Алгоритм DFS используется для нахождения циклов в графе.
## Алгоритм Дейкстры
- Основное использование Алгоритма Дейкстры - это оптимальный (кратчайший) маршрут между двумя произвольными точками. Например прокладывание оптимального маршрута между двумя точками на карте или сети дорог.
- Алгоритм Дейкстры может использоваться для оптимизации расписания задач. Например, у нас есть поставленные задачи, ограниченный по времени, также каждая задача может иметь определенные зависимости от других задач. При использовании данного Алгоритма, можно составить оптимальный порядок выполнения данных задач, для сокращения суммарного времени выполнения всех задач.
## Алгоритм Флойда-Уоршелла
- Алгоритм Флойда-Уоршелла может быть использован для оптимизации транспортных сетей. Например, есть какая-то транспортная сеть, где разные дороги имеют различные время путешествия. Алгоритм Флойда-Уоршелла поможет найти наиболее эффективные пути между всеми парами городов. Это может быть использовано для оптимизации грузоперевозок, или для улучшения времени обхода общественного транспорта.
## Алгоритм Прима
- Напомню, что Алгоритм Прима используется для нахождения остовного дерева в графе с минимальным весом. Это может быть использовано для определения оптимального маршрута коммуникационной сети. Например, возьмем газопровод соединяющий города, для того чтобы использовать минимальное количество материала для изготовления труб газопровода, используется Алгоритм Прима, чтобы соединить эти города сетью газопровода, максимально выгодным образом.
---
## Плюсы и минусы
## BFS
#### Плюсы:
- Простота реализации, так как BFS является одним из наиболее простых алгоритмов обхода графа.
- Удобство нахождения связанных компонентов, так как BFS сначала перебирает все доступные вершины и только потом переходит на следующий уровень, то таким образом можно найти всё вершины достижимые от заданной точки.
- Гарантирует нахождения кратчайшего пути в невзвешенном графе.
#### Минусы:
- Требует дополнительную память, так как нужно хранить порядок обхода вершин. Соответсвенно алгоритм требует по памяти О(V), где V - количество вершин в графе.
- Алгоритм бесполезен для графов с отрицательными весами, там как BFS не учитывает вес ребра.
- Не способен генерировать оптимальный путь для взвешенных графов. Путь может быть найден, но не факт, что он будет оптимальным.
## DFS
#### Плюсы:
- Простота реализации независимо от типа способа, на стеке или при помощи рекурсии.
- Эффективность, иногда DFS более предпочтителен нежели BFS, когда дело заходит о достижении определённой вершины
#### Минусы:
- Также как и BFS требует доп памяти О(V)
- Нет гарантии нахождения кратчайшего пути в невзвешенном графе
- Склонность к зацикливание, если у графа есть циклы
## Алгоритм Дейкстры
#### Плюсы:
- Эффективность, сложность алгоритма линейно-логарифмическая, что делает этот алгоритм эффективным на больших графах.
- Гарантия оптимальности. Алгоритм Дейкстры гарантирует нахождение кратчайших расстояний от стартовой до всех остальных.
#### Минусы:
- Требует положительный вес ребер. [Почему?](https://ru.stackoverflow.com/questions/758409/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC-%D0%94%D0%B5%D0%B9%D0%BA%D1%81%D1%82%D1%80%D1%8B-%D0%BE%D1%82%D1%80%D0%B8%D1%86%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5-%D1%80%D0%B5%D0%B1%D1%80%D0%BE-%D0%BD%D0%B0-%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%D0%B5)
- Требует полной информации о графе, количество вершин, вес рёбер должен быть известен.
## Алгоритм Флойда-Уоршелла
#### Плюсы:
- Гарантия нахождения кратчайших расстояний между всеми парами вершин.
- Эффективность для небольших графах
#### Минусы:
- Высокая сложность О(V^3).
- Неэффективность на больших графах, с большим количеством вершин.
- Дополнительная память, в виде матрицы {V, V}, что также для больших графов может быть критично.
## Алгоритм Прима
#### Плюсы:
- Гарантия нахождения минимального основного дерева для неориентированных графов
- Высокая эффективность для разреженных графов, когда количество рёбер меньше количества вершин. Это связано с тем, что алгоритм работает только с непосещенными ребрами.
#### Минусы:
- Неэффективность для плотных графов, так как алгоритм Прима анализирует рёбра, то количество рёбер близкое к максимально возможным делают этот алгоритм неэффективным.
- Дополнительная память О(V^2), что для графов с большим количество вершим может быть критично.