https://github.com/urtuba/cpp-binary-tree
constructing a binary tree structure and finding path on it
https://github.com/urtuba/cpp-binary-tree
binary-tree cpp data-structures homework istanbul-technical-university
Last synced: 5 months ago
JSON representation
constructing a binary tree structure and finding path on it
- Host: GitHub
- URL: https://github.com/urtuba/cpp-binary-tree
- Owner: urtuba
- License: mit
- Created: 2019-01-20T10:03:44.000Z (almost 7 years ago)
- Default Branch: master
- Last Pushed: 2021-07-12T19:13:39.000Z (over 4 years ago)
- Last Synced: 2025-03-16T00:26:45.481Z (9 months ago)
- Topics: binary-tree, cpp, data-structures, homework, istanbul-technical-university
- Language: C++
- Homepage:
- Size: 296 KB
- Stars: 1
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
README
# Binary Tree Exercise
It is data structures homework in Istanbul Technical University.
## Problem
There is an input file first line indicates values of nodes of the tree to be created. They are always placed like the graph given below:
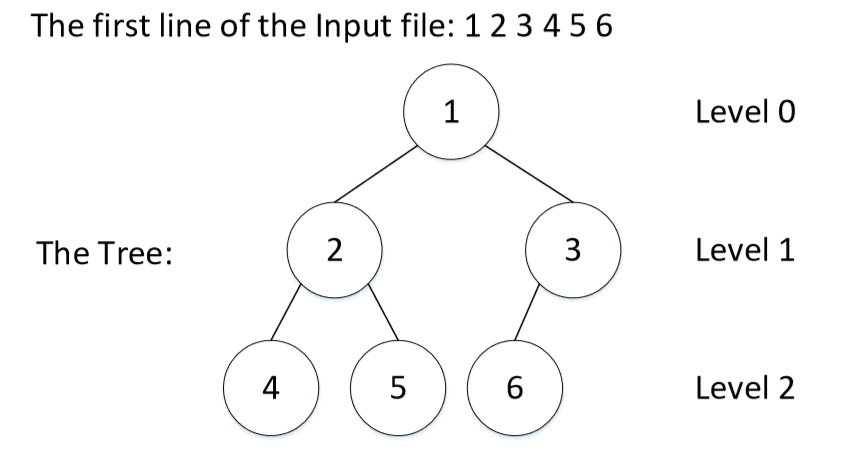
Left to right, top to bottom. It is impossible to add a node on level 3 before fully filling level 2. Or you cannot add new node to right if left is blank.
Second line of input file indicates the target. We will try to find a path in the left sub-tree and another one in right sub-tree which makes the target number whey you sum their nodes. Example:
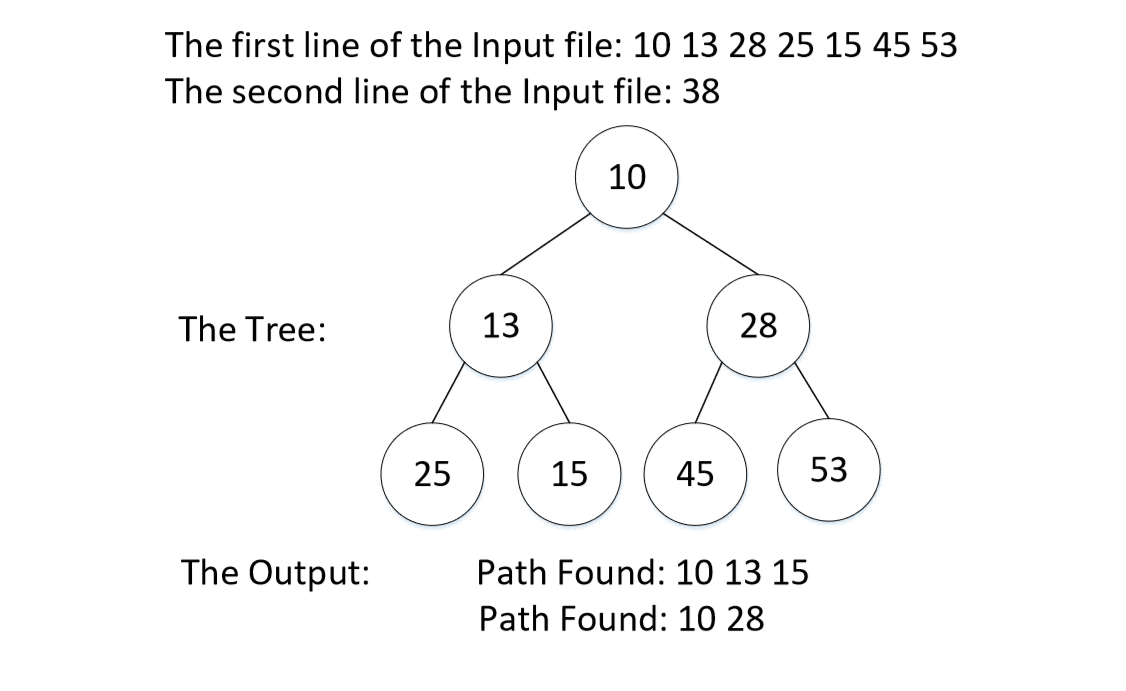
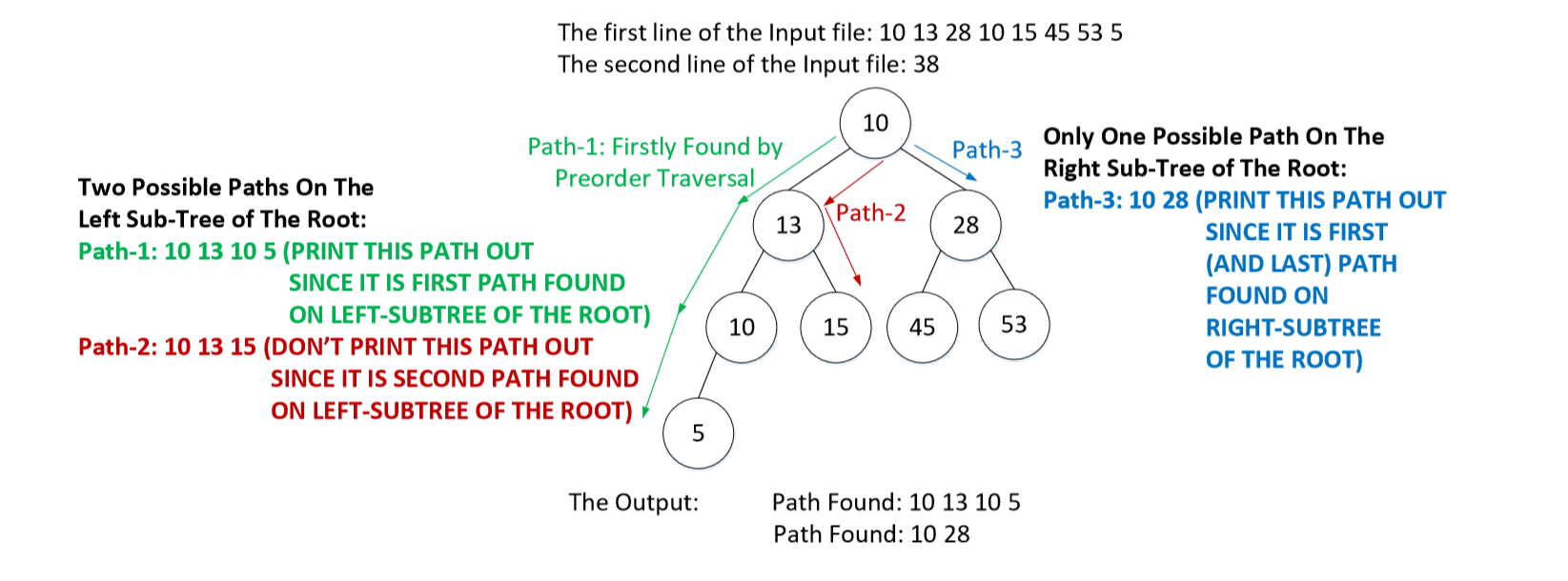
We need 1 path for each subtree. If program finds more than one, leftest path is valid in the subtree.
## Compile and Run
Compile it: ``g++ -std=c++11 -Wall -Werror b_tree.cpp -o b_tree ``
Run it: ``./b_tree input.txt``
Run on windows: ``b_tree input.txt``
## Notes
Remember the first image, there was a series of data like 1, 2, 3, 4, 5... As you can realize, this numbers are ordered with positive integers. Even tree is initialized with different data like 19, 25, 30... there is a secret 1, 2, 3 order in order to their position in the tree. I used this to distinguish whether a node is left or right subtree.
Whenever ``ptr -> nodeNum < 3*pow(2, floor(log2(ptr->nodeNum)))/2`` goes true, you can assume you are in left subtree.