https://github.com/vronnn/modul1_probstat_5025211142
https://github.com/vronnn/modul1_probstat_5025211142
Last synced: 2 months ago
JSON representation
- Host: GitHub
- URL: https://github.com/vronnn/modul1_probstat_5025211142
- Owner: vronnn
- Created: 2022-10-10T03:13:11.000Z (over 2 years ago)
- Default Branch: main
- Last Pushed: 2022-10-12T13:53:50.000Z (over 2 years ago)
- Last Synced: 2025-01-23T04:28:20.593Z (4 months ago)
- Language: R
- Size: 7.81 KB
- Stars: 1
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# **Modul1_Probstat_5025211142**
## **Nomor 1**
### **Seorang penyurvei secara acak memilih orang-orang di jalan sampai dia bertemu dengan seseorang yang menghadiri acara vaksinasi sebelumnya.**
a) Berapa peluang penyurvei bertemu x = 3 orang yang tidak menghadiri acara vaksinasi sebelum keberhasilan pertama ketika p = 0,20 dari populasi menghadiri acara vaksinasi ? (distribusi Geometrik)
> Peluang Distribusi Geometrik dapat diperoleh dengan fungsi `dgeom(x,p)` dengan `x` = sukses pertama dan `p` = peluang sukses
```R
x = 3
p = 0.20
paste("peluang : ", dgeom(x, p))
```
output :
```
peluang : 0.1024
```
b) Mean Distribusi Geometrik dengan 10000 data random , prob = 0,20 dimana distribusi geometrik acak tersebut X = 3 ( distribusi geometrik acak () == 3 )
> Distribusi Geometrik `n` data random dapat diperoleh menggunakan fungsi `rgeom()` dan mean dapat diperoleh menggunakan fungsi `mean()`
```R
n = 10000
paste("mean : ", mean(rgeom(n, p) == 3))
```
output :
```
mean : 0.0985
```
c) Bandingkan Hasil poin a dan b , apa kesimpulan yang bisa didapatkan?
```
hasil dari poin a adalah nilai konstan, sedangkan hasil dari poin b bernilai random atau selalu berubah-ubah namun selalu mendekati nilai dari poin a, kesimpulannya adalah mean dari distribusi geometrik yang menggunakan n data random akan berubah-ubah namun selalu mendekati nilai peluang distribusi geoemetriknya
```
d) Histogram Distribusi Geometrik , Peluang X = 3 gagal Sebelum Sukses Pertama
>Histogram Distribusi Geomestrik dapat ditampilkan menggunakan fungsi `hist()` sedangkan data random distribusinya dapat digenerate menggunakan fungsi `rgeom()`
```R
hist(rgeom(n,p), col = blues9)
```

e) Nilai Rataan (μ) dan Varian (σ²) dari Distribusi Geometrik.
> - nilai rataan (μ) Distribusi Geometrik = `1/p`
> - varian (σ²) Distribusi Geometrik = `(1-p)/p²`
```R
mean = 1/p
varians = (1-p)/p^2
paste("µ : ", mean)
paste("σ² : ", varians)
```
output :
```
µ : 5
σ² : 20
```
## **Nomor 2**
### **Terdapat 20 pasien menderita Covid19 dengan peluang sembuh sebesar 0.2. Tentukan :**
a) Peluang terdapat 4 pasien yang sembuh.
>Peluang Distribusi Binomial dapat diperoleh menggunakan fungsi `dbinom(x,n,p)` dengan `x` = sembuh, `n` = total pasien, dan `p` = peluang sembuh
```R
x = 4
n = 20
p = 0.2
paste("peluang : ", dbinom(x,n,p))
```
output :
```
peluang : 0.218199401946101
```
b) Gambarkan grafik histogram berdasarkan kasus tersebut.
>Histogram Distribusi Binomial dapat ditampilkan menggunakan fungsi `hist(x,n,p)` dengan `x` = banyak data random yang digenerate, `n` = jumlah sampel, dan `p` = peluang sembuh
```R
hist(rbinom(4,20,0.2), col = blues9)
```
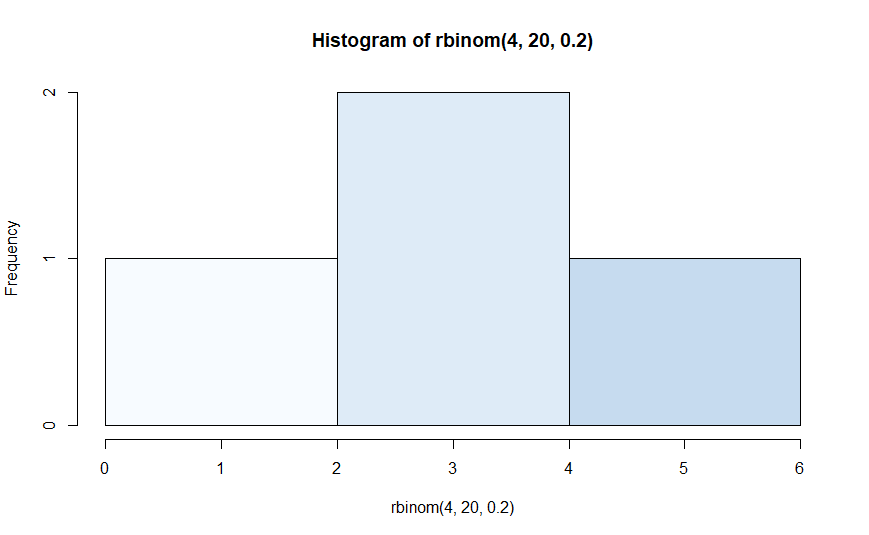
c) Nilai Rataan (μ) dan Varian (σ²) dari Distribusi Binomial.
> - nilai rataan (μ) Distribusi Binomial = `n*p`
> - varian (σ²) Distribusi Binomial = `n * p (1-p)`
```R
mean = n*p
varians = n*p*(1-p)
paste("µ : ", mean)
paste("σ² : ", varians)
```
output :
```
µ : 4
σ² : 3.2
```
## **Nomor 3**
### **Diketahui data dari sebuah tempat bersalin di rumah sakit tertentu menunjukkan rata-rata historis 4,5 bayi lahir di rumah sakit ini setiap hari. (gunakan Distribusi Poisson)**
a) Berapa peluang bahwa 6 bayi akan lahir di rumah sakit ini besok?
>Peluang Distribusi Poisson dapat diperoleh menggunakan fungsi `dpois(x,λ)` dengan `x` = jumlah lahir dan `λ` = rata-rata kelahiran
```R
x = 6
λ = 4.5
paste("peluang : ", dpois(x,λ))
```
output :
```
peluang : 0.128120143864584
```
b) Simulasikan dan buatlah histogram kelahiran 6 bayi akan lahir di rumah sakit ini selama setahun (n = 365)
>Histogram Distribusi Poisson dapat ditampilkan menggunakan fungsi `hist()` sedangkan data kelahiran selama `n` hari dapat digenerate menggunakan fungsi `rpois(n,λ)`
```R
n = 365
hist(rpois(n,λ), col = blues9)
```

c) dan bandingkan hasil poin a dan b , Apa kesimpulan yang bisa didapatkan
```
hasil dari poin a akan selalu bernilai konstan, sedangkan hasil dari poin b menunjukan sebaran nilai yang mendekati nilai λ dan apabila dicari meannya, hasilnya akan sama dengan λ, kesimpulannya adalah mean dari hasil sebaran data poin b akan sama dengan λ di poin a sehingga apabila dicari peluang distribusi poisson dari mean yang didapat dari poin b, hasilnya akan sama dengan poin a
```
d) Nilai Rataan (μ) dan Varian (σ²) dari Distribusi Poisson.
> - nilai rataan (μ) Distribusi Poisson = `λ`
> - varian (σ²) Distribusi Poisson = `λ`
```R
mean = λ
varians = λ
paste("µ : ", mean)
paste("σ² : ", varians)
```
output :
```
µ : 4.5
σ² : 4.5
```
## **Nomor 4**
### **Diketahui nilai x = 2 dan v = 10. Tentukan:**
a) Fungsi Probabilitas dari Distribusi Chi-Square.
>Probabilitas Distribusi Chi-Square dapat diperoleh menggunakan fungsi `dchisq(x,v)`
```R
x = 2
v = 10
paste("pdf : ", dchisq(x,v))
```
output :
```
pdf : 0.00766415502440505
```
b) Histogram dari Distribusi Chi-Square dengan 100 data random.
>Histogram Distribusi Chi-Square dapat ditampilkan menggunakan fungsi `hist()` sedangkan data random Distribusi Chi-Square dapat digenerate menggunakan fungsi `rchisq()`
```R
n = 100
hist(rchisq(100,v,ncp=0), col = blues9)
```
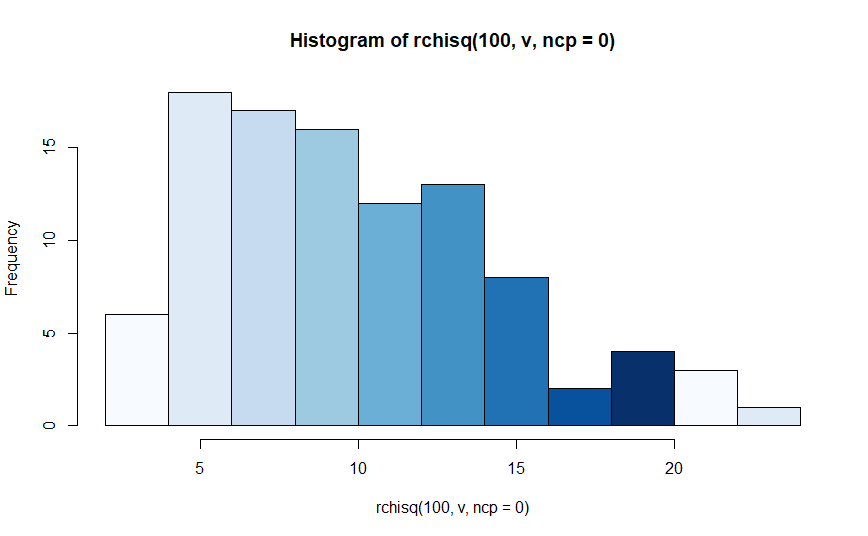
c) Nilai Rataan (μ) dan Varian (σ²) dari Distribusi Chi-Square.
> - nilai rataan (μ) Distribusi Chi-Square = `v`
> - varian (σ²) Distribusi Chi-Square = `2*v`
```R
mean = v
varians = 2*v
paste("µ : ", mean)
paste("σ² : ", varians)
```
output :
```
µ : 10
σ² : 20
```
## **Nomor 5**
### **Diketahui bilangan acak (random variable) berdistribusi exponential (λ = 3). Tentukan**
a) Fungsi Probabilitas dari Distribusi Exponensial
>Probabilitas Distribusi Exponensial dapat diperoleh menggunakan fungsi `dexp(x,λ)`
```R
λ = 3
paste(dexp(10,λ))
```
output :
```
2.80728689065205e-13
```
b) Histogram dari Distribusi Exponensial untuk 10, 100, 1000 dan 10000 bilangan random
>Histogram Distribusi Exponensial dapat ditampilkan menggunakan fungsi `hist()` sedangkan data random Distribusi Exponensial dapat digenerate menggunakan fungsi `rexp(n,λ)` dengan `n` = banyak data
```R
par(mfrow = c(2,2))
hist(rexp(10,λ), col = blues9)
hist(rexp(100,λ), col = blues9)
hist(rexp(1000,λ), col = blues9)
hist(rexp(10000,λ), col = blues9)
```

c) Nilai Rataan (μ) dan Varian (σ²) dari Distribusi Exponensial untuk n = 100 dan λ = 3
### petunjuk :
- Gunakan set.seed(1)
- Gunakan fungsi bawaan R
> - nilai rataan (μ) Distribusi Exponensial dapat dicari menggunakan fungsi `mean()`
> - varian (σ²) Distribusi Eksponensial dapat dicari menggunakan fungsi `var()`
```R
set.seed(1)
paste("rataan : ", mean(rexp(100,λ)))
set.seed(1)
paste("varian : ", var(rexp(100,λ)))
```
output :
```
rataan : 0.343558812019206
varian : 0.0974443032622406
```
## **Nomor 6**
### **Diketahui generate random nilai sebanyak 100 data, mean = 50, sd = 8. Tentukan**
a) Fungsi Probabilitas dari Distribusi Normal P(X1 ≤ x ≤ X2), hitung Z-Score Nya dan plot data generate randomnya dalam bentuk grafik. Petunjuk(gunakan fungsi plot()).
Keterangan :
- X1 = Dibawah rata-rata
- X2 = Diatas rata-rata
- Contoh data :
1,2,4,2,6,3,10,11,5,3,6,8
- rata-rata = 5.083333
- X1 = 5
- X2 = 6
>Probabilitas Distribusi Normal dapat diperoleh menggunakan fungsi `dnorm(n,µ,sd)` dengan `n` = jumlah data, `µ` = mean, dan `sd` = standar deviasi
```
n = 100
µ = 50
sd = 8
paste("pdf : ", dnorm(n,µ,sd))
par(mfrow = c(1,1))
set.seed(1)
random <- rnorm(n,µ,sd)
x1 = floor(mean(random))
x2 = ceiling(mean(random))
z1 = (x1 - µ)/sd
z2 = (x2 - µ)/sd
plot(random, col="blue")
```
output :
```
pdf : 1.64250227269486e-10
z1 : 0
z2 : 0.125
```

b) Generate Histogram dari Distribusi Normal dengan breaks 50 dan format penamaan:
NRP_Nama_Probstat_{Nama Kelas}_DNhistogram
- Contoh :
312312312_Rola_Probstat_A_DNhistogram
>Histogram Distribusi Normal dapat ditampilkan menggunakan fungsi `hist()` sedangkan data random Distribusi Normal dapat digenerate menggunakan fungsi `rnorm()`
```R
par(mfrow = c(1,1))
hist(rnorm(n,µ,sd), breaks = 50, main = "5025211142_Mohammad Zhafran Dzaky_Probstat_A_DNhistogram", col = blues9)
```

c) Nilai Varian (σ²) dari hasil generate random nilai Distribusi Normal.
> - varian (σ²) Distribusi Normal dapat diperoleh menggunakan fungsi `var()`
```R
set.seed(1)
paste("varian : ", var(rnorm(n,µ,sd)))
```