https://github.com/yanqiangmiffy/machine-learning
essential principles to help you get a better understanding of machine learning
https://github.com/yanqiangmiffy/machine-learning
Last synced: 3 months ago
JSON representation
essential principles to help you get a better understanding of machine learning
- Host: GitHub
- URL: https://github.com/yanqiangmiffy/machine-learning
- Owner: yanqiangmiffy
- Created: 2021-08-01T19:04:46.000Z (about 4 years ago)
- Default Branch: main
- Last Pushed: 2021-07-27T13:25:12.000Z (about 4 years ago)
- Last Synced: 2025-02-24T01:17:01.610Z (8 months ago)
- Size: 5.62 MB
- Stars: 0
- Watchers: 1
- Forks: 0
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
Awesome Lists containing this project
README
# 又出新模型了?本文教你以不变应万变
## 频率派的最大似然估计和贝叶斯派的最大后验估计
(摘自软绵绵的小熊猫)
它们都是参数估计的方法,都是对模型的参数进行求解。
* 频率派把未知参数看成普通变量,把样本看成随机变量。
* 概率就是某一个随机试验进行无穷次重复,然后统计发生的频率。样本空间可以无限大,可以有放回无限反复抽取。
* 预测一个小时后上海会不会下雨,对于统计学比较拉胯的情况,贝叶斯派优势体现出来。
* 频率派和贝叶斯派最大的区别就在于对于随机变量如何看待。
频率派认为随机变量是一个固定的值(就是一个普通的变量)
贝叶斯派认为变量一开始即服从某一分布,我们观测到的值就是分布的不断叠加,这样的叠加就意味着对参数分布的估计会产生变化
机器学习案例当中的做法:
不管用什么方法,最终都要落实到模型的求解上来,也就是给我一些数据,我们来求解模型和参数。
以扔硬币为例:
抛一枚硬币,十次,9次正面,1次反面。有的人认为硬币就是均匀的。这里的先验知识是什么呢?最大后验又是什么。
#### 一)频率派求解模型参数的做法:
三步走——1)设计模型,2)设计损失函数,3)具体的参数求解(牛顿法、梯度下降、直接给出解析解)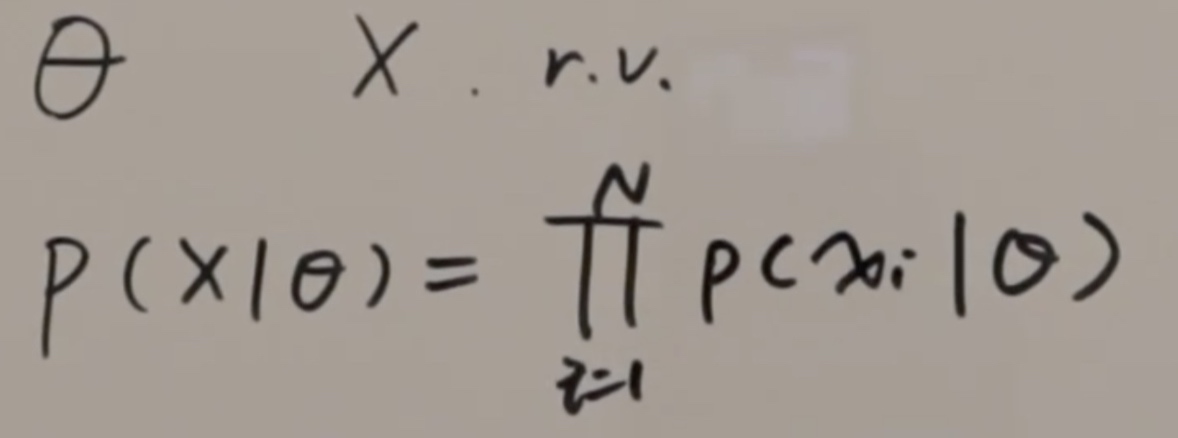
公式中,theta是未知常量,也就是我们要求的硬币正面朝上的概率,X是一个随机变量,即扔硬币试验的结果,它们是独立无关的。
我们要做的就是通过X反过来求theta。又因为在若干次实验中,事件是真实发生了,那么这些事件同时发生的概率该如何计算呢?当然是直接相乘。公式中P代表二项分布。argmax是似然函数,我们要求得它最大同时得到theta的估计,这个叫做极大似然估计。那我们对它求极值就可以得到我们需要的theta,也就是我们这里硬币正面朝上的几率。有的时候为了方便求解,会加上log函数,叫做log似然函数。这就是频率派求解模型参数的做法,就是上面说过的三步走——1)设计模型,2)设计损失函数,3)具体的参数求解(牛顿法、梯度下降、直接给出解析解)
这是所有的频率派极大似然估计的套路,这类模型本质是统计学问题,目的是做参数估计。
#### 二)贝叶斯学派求解模型参数的做法:
问题在于theta不是一个固定的值,它是一个分布。这里面假设它是一个分布,叫做p。我们要求的什么呢?我们在已有数据条件下,让后验概率最大,那我们借助贝叶斯公式来求它。px是整个样本空间,我们关心的是左边最大值时候的theta,所以我们要求的是参数,和分母无关,所以可以理解成它的最大值其实正比于整个分子。
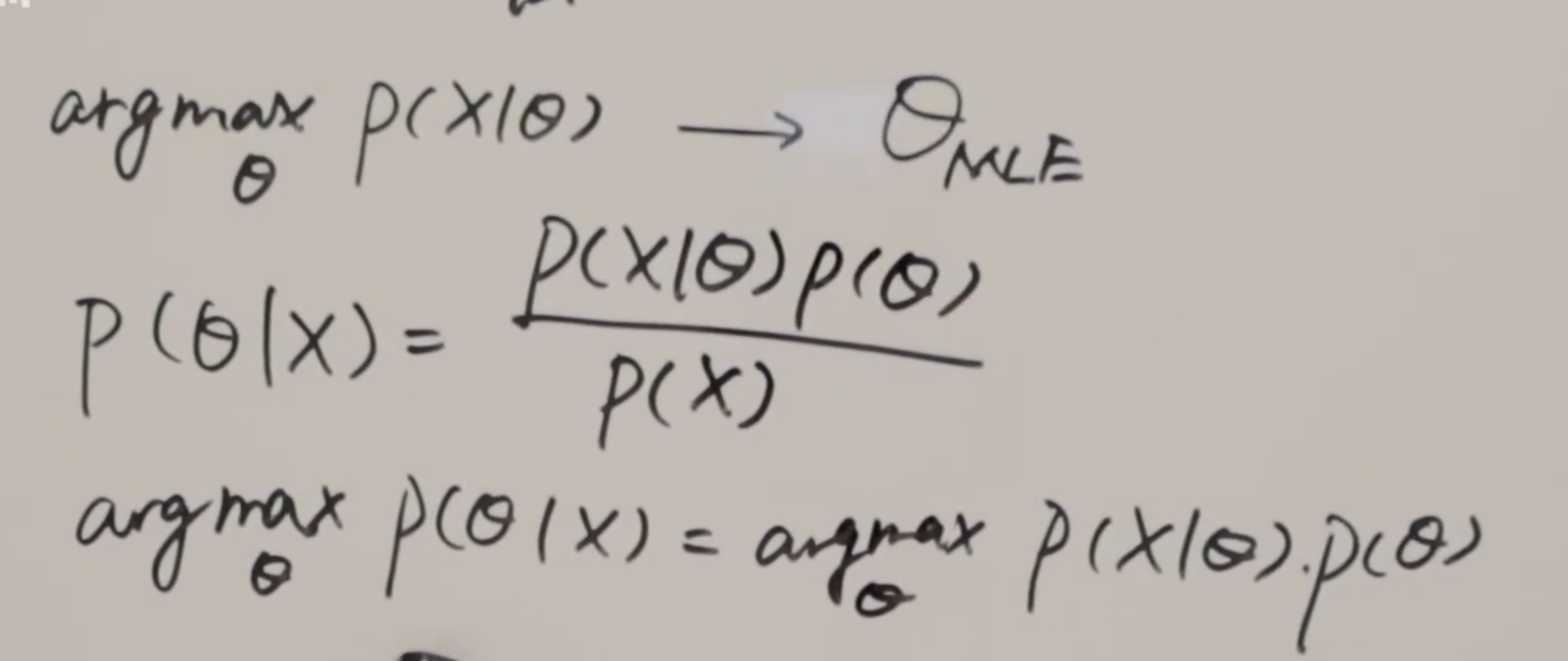就是这样。这是最大后验估计得出来的结果。
后验概率最大,关心的是左边最大值时的theta,我们要求的是参数和分母无关。
最大后验估计只是贝叶斯派的一种参数估计的方法,因为应用了贝叶斯公式是为了求theta而不是完全的贝叶斯派。
什么是完全的贝叶斯派?其实就是贝叶斯估计或者叫贝叶斯预测,我们要求的就是完整的后验概率的计算,就是要把刚才和theta无关的分母求出来。把整个后验概率求出来之后,有什么用处呢?求出后验概率之后,就可以借助theta来完成对一个新样本的预测。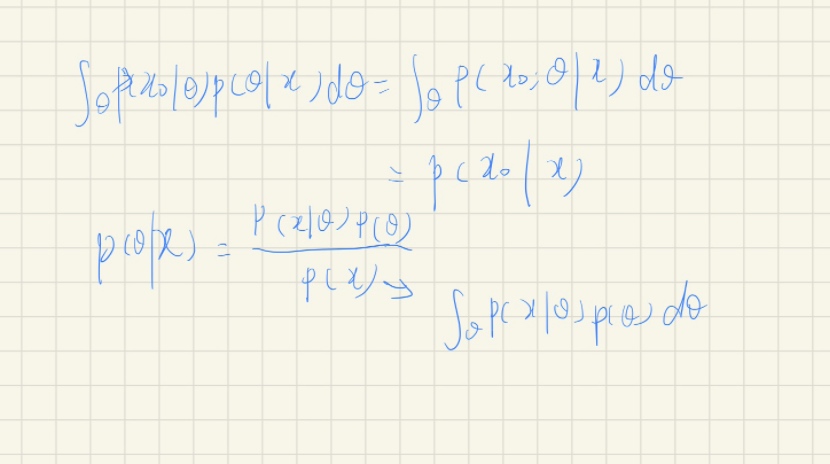
这样就可以对x0这样的新样本来预测它的结果。换句话说,不止关心模型的参数theta,更加关心的是一个端到端的问题。从所有已知的数据当中求解新样本的概率。这一部分有点边缘概率的意思,我们计算得到新样本的预测结果,这是真正的贝叶斯预测。
真正的贝叶斯预测是非常难做的,因为我们在刚才的最大后验估计中,忽略的分母部分其实需要完整的把它算出来,然后做一个对参数空间的积分。那这里面这个积分其实是非常难求的,甚至很多时候解析解找不到,只能用一些数值积分的方法,比如说一些采样的方法能够把它解出来,后面会在概率图模型当中详细讲解,这里先跳过。现在只需要知道完整的贝叶斯预测求解非常困难,需要用到一些数值积分的方法就可以。

贝叶斯派的最大后验估计,仔细看就会发现其中有一部分就是前面提到的极大似然估计,另外的部分其实就是我们对参数的默认分布的假设,这里也叫先验。
# 谁是对的?下面的推导会证明,频率派极大似然估计加上L2正则化之后,和贝叶斯派最大后验估计,结果一致!
回到核心问题上,频率派 vs 贝叶斯派,极大似然估计 vs 最大后验估计。只要先验不总是为1,那么这两个式子估计出来的结果就不一样。那么谁是对的呢?回到上面抛硬币的例子,抛了10次有9次正面朝上,有的人觉得是0.9,完全按前面统计结果推算————就是上面MLE公式;有的人完全按照自己的直觉,按照自己多年来对硬币的了解,按照自己的先验知识,觉得应该在0.9基础上进行修正————就是下面MAP公式。
到这里,看起来好像还是贝叶斯派好。频率派看起来做到了尊重事实,但是很容易收到样本数量不足的影响,这也就是机器学习频率派统计学习方法中的过拟合的表现。
**那面对过拟合怎么办呢?样本数量没法增加了————上正则化!**那上正则化会变成什么样子,下面来研究一个线性回归的例子。
#### 一)频率派的做法
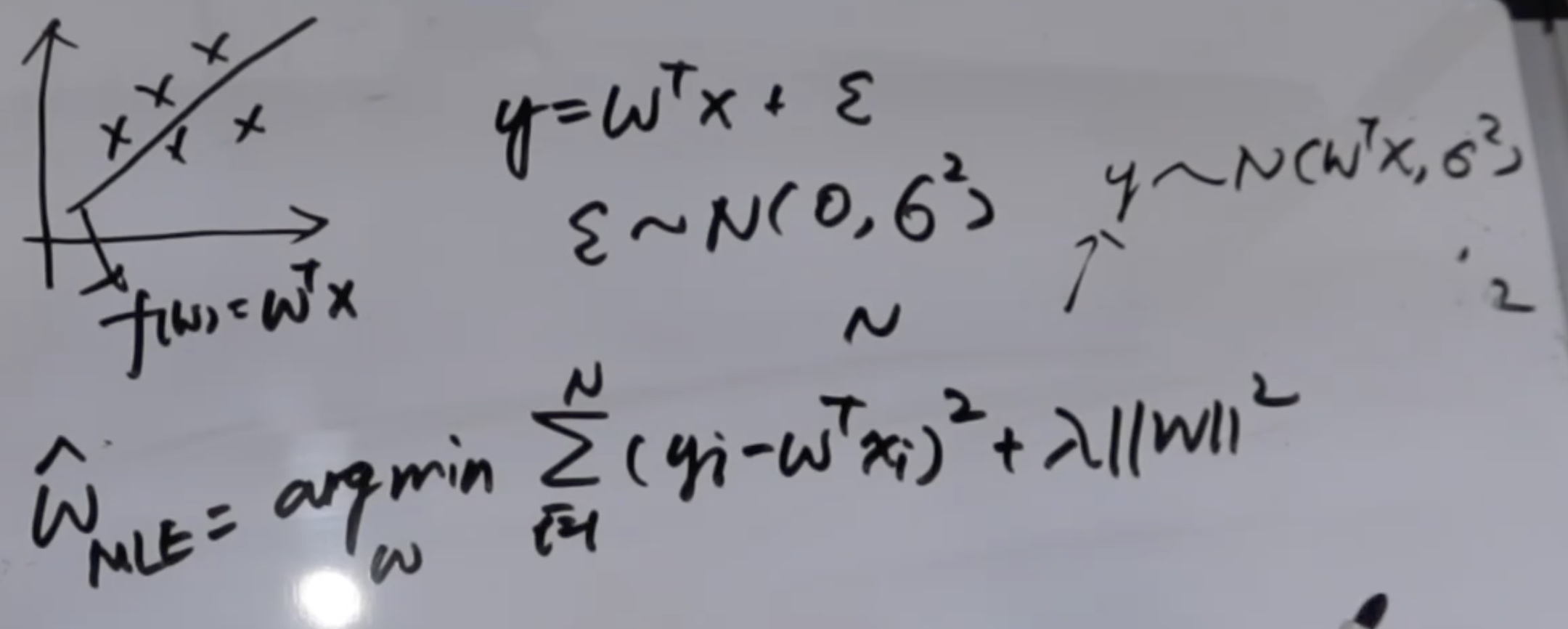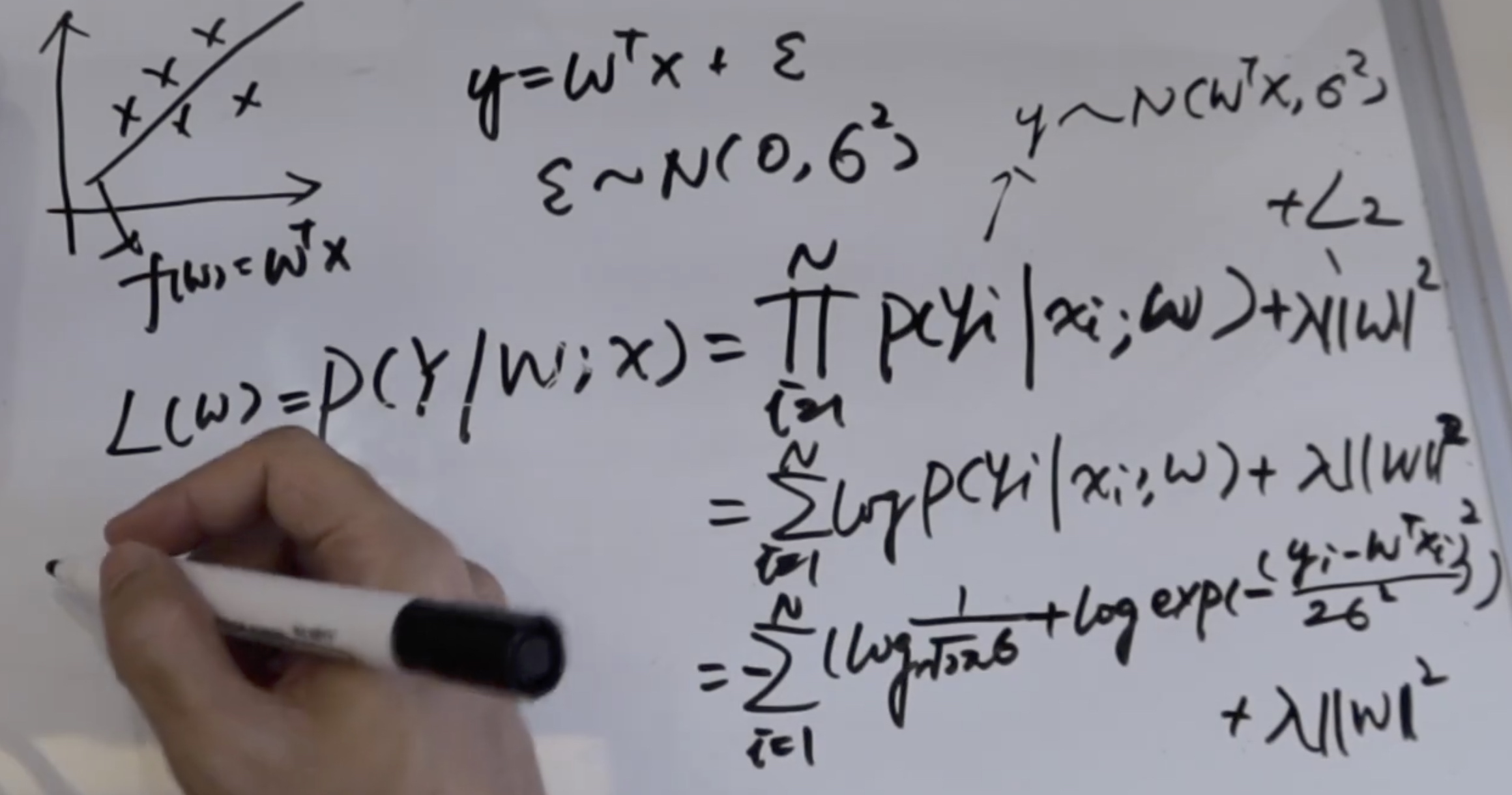**这是在线性回归问题中,假设误差服从高斯分布的,频率派极大似然估计,为了防止过拟合加上L2正则化,得到的参数解。**
#### 二)贝叶斯派的做法
既然是贝叶斯派,那我们就需要假定有一个W的先验,这里我们先假设w服从一个正态分布, 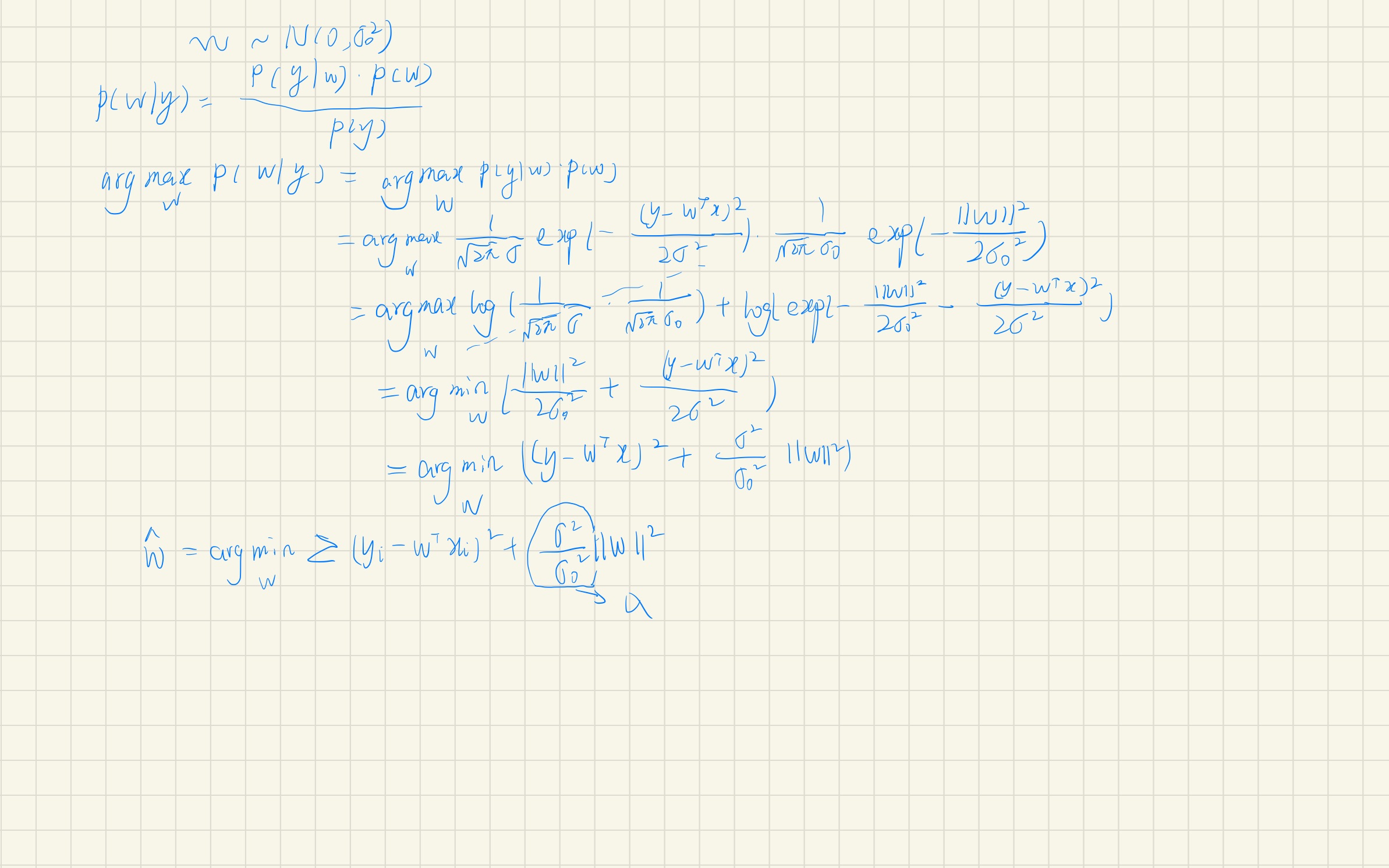
####三)结论:
对于线性回归,模型的参数(先验)服从高斯分布的情况下,**最大后验估计的计算结果**与**加上L2正则化的极大似然估计的估算结果**是一致的。
PS:如果模型的参数服从的不是高斯分布,如果是拉普拉斯分布,那么最大后验估计的结果与L1正则化的极大似然估计的结果又会保持一致。
面对样本过少带来的过拟合,频率派通常会使用正则化的技巧,来使模型变得更稳定,泛化能力更强。那贝叶斯派的最大后验估计,则对参数使用不同的先验分布来进行校正。
1. 为什么在推导过程中假设误差服从正态分布
2. 为什么L2正则化对应的先验是正态分布,L1正则化对应的是拉普拉斯分布;这两者对应的背后有什么样的数学解释,揭示了什么样的本质
下一期讲你见过的机器学习模型中,哪些模型是频率派做法,哪些模型又是贝叶斯派做法。这些频率派模型当中,它们的损失函数为什么要这么设计;贝叶斯派做法当中,它们又是如何引入先验分布的,它们为什么引入这样的先验分布。