Ecosyste.ms: Awesome
An open API service indexing awesome lists of open source software.
https://github.com/zrwusa/data-structure-typed
Javascript Data Structure & TypeScript Data Structure. Heap, Binary Tree, Red Black Tree, Linked List, Deque, Trie, HashMap, Directed Graph, Undirected Graph, Binary Search Tree, AVL Tree, Priority Queue, Graph, Queue, Tree Multiset, Singly Linked List, Doubly Linked List, Max Heap, Max Priority Queue, Min Heap, Min Priority Queue, Stack.
https://github.com/zrwusa/data-structure-typed
avl-tree binary-search-tree binary-tree data-structures deapth-first-search deque dequeue dijkstra-algorithm directed-graph floyd-warshall-algorithm graph heap javascript-data-structures linked-list red-black-tree
Last synced: 3 days ago
JSON representation
Javascript Data Structure & TypeScript Data Structure. Heap, Binary Tree, Red Black Tree, Linked List, Deque, Trie, HashMap, Directed Graph, Undirected Graph, Binary Search Tree, AVL Tree, Priority Queue, Graph, Queue, Tree Multiset, Singly Linked List, Doubly Linked List, Max Heap, Max Priority Queue, Min Heap, Min Priority Queue, Stack.
- Host: GitHub
- URL: https://github.com/zrwusa/data-structure-typed
- Owner: zrwusa
- License: mit
- Created: 2023-06-15T16:32:49.000Z (over 1 year ago)
- Default Branch: main
- Last Pushed: 2024-12-05T21:38:56.000Z (about 2 months ago)
- Last Synced: 2025-01-12T01:03:24.074Z (10 days ago)
- Topics: avl-tree, binary-search-tree, binary-tree, data-structures, deapth-first-search, deque, dequeue, dijkstra-algorithm, directed-graph, floyd-warshall-algorithm, graph, heap, javascript-data-structures, linked-list, red-black-tree
- Language: TypeScript
- Homepage: https://data-structure-typed-docs.vercel.app
- Size: 36.3 MB
- Stars: 135
- Watchers: 1
- Forks: 9
- Open Issues: 20
-
Metadata Files:
- Readme: README.md
- Changelog: CHANGELOG.md
- Contributing: CONTRIBUTING.md
- License: LICENSE
- Code of conduct: CODE_OF_CONDUCT.md
- Security: SECURITY.md
Awesome Lists containing this project
README
# data-structure-typed
[//]: # ()
[//]: # (
)
> ***Our goal is to make every data structure as convenient and efficient as JavaScript's Array.***
## Installation and Usage
### npm
```bash
npm i data-structure-typed --save
```
### yarn
```bash
yarn add data-structure-typed
```
```js
import {
Heap, Graph, Queue, Deque, PriorityQueue, BST, Trie, DoublyLinkedList,
AVLTree, SinglyLinkedList, DirectedGraph, RedBlackTree, TreeMultiMap,
DirectedVertex, Stack, AVLTreeNode
} from 'data-structure-typed';
```
If you only want to use a specific data structure independently, you can install it separately, for example, by running
```bash
npm i heap-typed --save
```
## Why
Do you envy C++ with [STL]() (std::), Python with [collections](), and Java with [java.util]() ? Well, no need to envy
anymore! JavaScript and TypeScript now have [data-structure-typed]().**`Benchmark`** compared with C++ STL.
**`API standards`** aligned with ES6 and Java. **`Usability`** is comparable to Python
[//]: # ()
[//]: # ()
[//]: # ()
[//]: # ()
### Performance
Performance surpasses that of native JS/TS
Method
Time Taken
Data Scale
Belongs To
big O
Queue.push & shift
5.83 ms
100K
Ours
O(1)
Array.push & shift
2829.59 ms
100K
Native JS
O(n)
Deque.unshift & shift
2.44 ms
100K
Ours
O(1)
Array.unshift & shift
4750.37 ms
100K
Native JS
O(n)
HashMap.set
122.51 ms
1M
Ours
O(1)
Map.set
223.80 ms
1M
Native JS
O(1)
Set.add
185.06 ms
1M
Native JS
O(1)
### Plain language explanations
Data Structure
Plain Language Definition
Diagram
Linked List (Singly Linked List)
A line of bunnies, where each bunny holds the tail of the bunny in front of it (each bunny only knows the name of the bunny behind it). You want to find a bunny named Pablo, and you have to start searching from the first bunny. If it's not Pablo, you continue following that bunny's tail to the next one. So, you might need to search n times to find Pablo (O(n) time complexity). If you want to insert a bunny named Remi between Pablo and Vicky, it's very simple. You just need to let Vicky release Pablo's tail, let Remi hold Pablo's tail, and then let Vicky hold Remi's tail (O(1) time complexity).
Array
A line of numbered bunnies. If you want to find the bunny named Pablo, you can directly shout out Pablo's number 0680 (finding the element directly through array indexing, O(1) time complexity). However, if you don't know Pablo's number, you still need to search one by one (O(n) time complexity). Moreover, if you want to add a bunny named Vicky behind Pablo, you will need to renumber all the bunnies after Vicky (O(n) time complexity).
Queue
A line of numbered bunnies with a sticky note on the first bunny. For this line with a sticky note on the first bunny, whenever we want to remove a bunny from the front of the line, we only need to move the sticky note to the face of the next bunny without actually removing the bunny to avoid renumbering all the bunnies behind (removing from the front is also O(1) time complexity). For the tail of the line, we don't need to worry because each new bunny added to the tail is directly given a new number (O(1) time complexity) without needing to renumber all the previous bunnies.
Deque
A line of grouped, numbered bunnies with a sticky note on the first bunny. For this line, we manage it by groups. Each time we remove a bunny from the front of the line, we only move the sticky note to the next bunny. This way, we don't need to renumber all the bunnies behind the first bunny each time a bunny is removed. Only when all members of a group are removed do we reassign numbers and regroup. The tail is handled similarly. This is a strategy of delaying and batching operations to offset the drawbacks of the Array data structure that requires moving all elements behind when inserting or deleting elements in the middle.
Doubly Linked List
A line of bunnies where each bunny holds the tail of the bunny in front (each bunny knows the names of the two adjacent bunnies). This provides the Singly Linked List the ability to search forward, and that's all. For example, if you directly come to the bunny Remi in the line and ask her where Vicky is, she will say the one holding my tail behind me, and if you ask her where Pablo is, she will say right in front.
Stack
A line of bunnies in a dead-end tunnel, where bunnies can only be removed from the tunnel entrance (end), and new bunnies can only be added at the entrance (end) as well.
Binary Tree
As the name suggests, it's a tree where each node has at most two children. When you add consecutive data such as [4, 2, 6, 1, 3, 5, 7], it will be a complete binary tree. When you add data like [4, 2, 6, null, 1, 3, null, 5, null, 7], you can specify whether any left or right child node is null, and the shape of the tree is fully controllable.
Binary Search Tree (BST)
A tree-like rabbit colony composed of doubly linked lists where each rabbit has at most two tails. These rabbits are disciplined and obedient, arranged in their positions according to a certain order. The most important data structure in a binary tree (the core is that the time complexity for insertion, deletion, modification, and search is O(log n)). The data stored in a BST is structured and ordered, not in strict order like 1, 2, 3, 4, 5, but maintaining that all nodes in the left subtree are less than the node, and all nodes in the right subtree are greater than the node. This order provides O(log n) time complexity for insertion, deletion, modification, and search. Reducing O(n) to O(log n) is the most common algorithm complexity optimization in the computer field, an exponential improvement in efficiency. It's also the most efficient way to organize unordered data into ordered data (most sorting algorithms only maintain O(n log n)). Of course, the binary search trees we provide support organizing data in both ascending and descending order. Remember that basic BSTs do not have self-balancing capabilities, and if you sequentially add sorted data to this data structure, it will degrade into a list, thus losing the O(log n) capability. Of course, our addMany method is specially handled to prevent degradation. However, for practical applications, please use Red-black Tree or AVL Tree as much as possible, as they inherently have self-balancing functions.
Red-black Tree
A tree-like rabbit colony composed of doubly linked lists, where each rabbit has at most two tails. These rabbits are not only obedient but also intelligent, automatically arranging their positions in a certain order. A self-balancing binary search tree. Each node is marked with a red-black label. Ensuring that no path is more than twice as long as any other (maintaining a certain balance to improve the speed of search, addition, and deletion).
AVL Tree
A tree-like rabbit colony composed of doubly linked lists, where each rabbit has at most two tails. These rabbits are not only obedient but also intelligent, automatically arranging their positions in a certain order, and they follow very strict rules. A self-balancing binary search tree. Each node is marked with a balance factor, representing the height difference between its left and right subtrees. The absolute value of the balance factor does not exceed 1 (maintaining stricter balance, which makes search efficiency higher than Red-black Tree, but insertion and deletion operations will be more complex and relatively less efficient).
Heap
A special type of complete binary tree, often stored in an array, where the children nodes of the node at index i are at indices 2i+1 and 2i+2. Naturally, the parent node of any node is at ⌊(i−1)/2⌋.
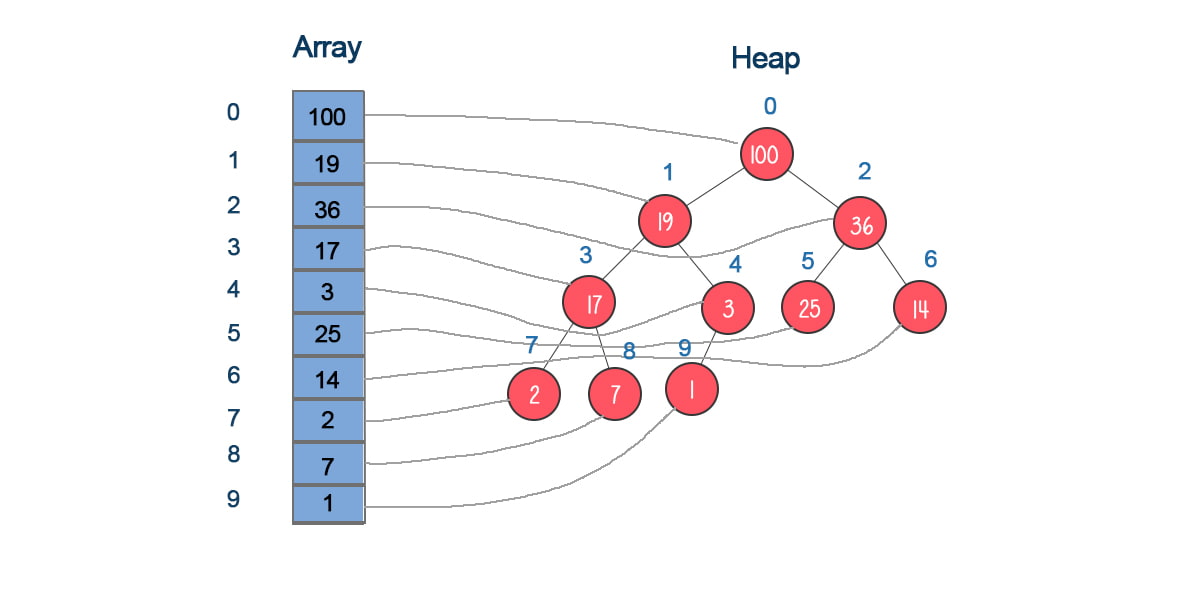
Priority Queue
It's actually a Heap.
Graph
The base class for Directed Graph and Undirected Graph, providing some common methods.
Directed Graph
A network-like bunny group where each bunny can have up to n tails (Singly Linked List).
Undirected Graph
A network-like bunny group where each bunny can have up to n tails (Doubly Linked List).
### Conciseness and uniformity
In [java.utils](), you need to memorize a table for all sequential data structures(Queue, Deque, LinkedList),
Java ArrayList
Java Queue
Java ArrayDeque
Java LinkedList
add
offer
push
push
remove
poll
removeLast
removeLast
remove
poll
removeFirst
removeFirst
add(0, element)
offerFirst
unshift
unshift
whereas in our [data-structure-typed](), you **only** need to remember four methods: `push`, `pop`, `shift`, and `unshift` for all sequential data structures(Queue, Deque, DoublyLinkedList, SinglyLinkedList and Array).
### Data structures available
We provide data structures that are not available in JS/TS
Data Structure
Unit Test
Perf Test
API Doc
NPM
Downloads
Binary Search Tree (BST)
Docs
NPM
Hash Map
Docs
Segment Tree
Binary Indexed Tree
## Vivid Examples
### AVL Tree
[Try it out](https://vivid-algorithm.vercel.app/), or you can run your own code using
our [visual tool](https://github.com/zrwusa/vivid-algorithm)
### Tree Multi Map
[Try it out](https://vivid-algorithm.vercel.app/)
### Directed Graph
[Try it out](https://vivid-algorithm.vercel.app/algorithm/graph/)
### Map Graph
[Try it out](https://vivid-algorithm.vercel.app/algorithm/graph/)
## Code Snippets
### Red Black Tree snippet
#### TS
```ts
import { RedBlackTree } from 'data-structure-typed';
const rbTree = new RedBlackTree();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced(); // true
rbTree.delete(10);
rbTree.isAVLBalanced(); // true
rbTree.print()
// ___6________
// / \
// ___4_ ___11________
// / \ / \
// _2_ 5 _8_ ____14__
// / \ / \ / \
// 1 3 7 9 12__ 15__
// \ \
// 13 16
```
#### JS
```js
import { RedBlackTree } from 'data-structure-typed';
const rbTree = new RedBlackTree();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced(); // true
rbTree.delete(10);
rbTree.isAVLBalanced(); // true
rbTree.print()
// ___6________
// / \
// ___4_ ___11________
// / \ / \
// _2_ 5 _8_ ____14__
// / \ / \ / \
// 1 3 7 9 12__ 15__
// \ \
// 13 16
```
### Free conversion between data structures.
```js
const orgArr = [6, 1, 2, 7, 5, 3, 4, 9, 8];
const orgStrArr = ["trie", "trial", "trick", "trip", "tree", "trend", "triangle", "track", "trace", "transmit"];
const entries = [[6, "6"], [1, "1"], [2, "2"], [7, "7"], [5, "5"], [3, "3"], [4, "4"], [9, "9"], [8, "8"]];
const queue = new Queue(orgArr);
queue.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const deque = new Deque(orgArr);
deque.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const sList = new SinglyLinkedList(orgArr);
sList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const dList = new DoublyLinkedList(orgArr);
dList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const stack = new Stack(orgArr);
stack.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const minHeap = new MinHeap(orgArr);
minHeap.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]
const maxPQ = new MaxPriorityQueue(orgArr);
maxPQ.print();
// [9, 8, 4, 7, 5, 2, 3, 1, 6]
const biTree = new BinaryTree(entries);
biTree.print();
// ___6___
// / \
// ___1_ _2_
// / \ / \
// _7_ 5 3 4
// / \
// 9 8
const bst = new BST(entries);
bst.print();
// _____5___
// / \
// _2_ _7_
// / \ / \
// 1 3_ 6 8_
// \ \
// 4 9
const rbTree = new RedBlackTree(entries);
rbTree.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const avl = new AVLTree(entries);
avl.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const treeMulti = new TreeMultiMap(entries);
treeMulti.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const hm = new HashMap(entries);
hm.print()
// [[6, "6"], [1, "1"], [2, "2"], [7, "7"], [5, "5"], [3, "3"], [4, "4"], [9, "9"], [8, "8"]]
const rbTreeH = new RedBlackTree(hm);
rbTreeH.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const pq = new MinPriorityQueue(orgArr);
pq.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]
const bst1 = new BST(pq);
bst1.print();
// _____5___
// / \
// _2_ _7_
// / \ / \
// 1 3_ 6 8_
// \ \
// 4 9
const dq1 = new Deque(orgArr);
dq1.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const rbTree1 = new RedBlackTree(dq1);
rbTree1.print();
// _____5___
// / \
// _2___ _7___
// / \ / \
// 1 _4 6 _9
// / /
// 3 8
const trie2 = new Trie(orgStrArr);
trie2.print();
// ['trie', 'trial', 'triangle', 'trick', 'trip', 'tree', 'trend', 'track', 'trace', 'transmit']
const heap2 = new Heap(trie2, { comparator: (a, b) => Number(a) - Number(b) });
heap2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const dq2 = new Deque(heap2);
dq2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const entries2 = dq2.map((el, i) => [i, el]);
const avl2 = new AVLTree(entries2);
avl2.print();
// ___3_______
// / \
// _1_ ___7_
// / \ / \
// 0 2 _5_ 8_
// / \ \
// 4 6 9
```
### Binary Search Tree (BST) snippet
```ts
import { BST, BSTNode } from 'data-structure-typed';
const bst = new BST();
bst.add(11);
bst.add(3);
bst.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5]);
bst.size === 16; // true
bst.has(6); // true
const node6 = bst.getNode(6); // BSTNode
bst.getHeight(6) === 2; // true
bst.getHeight() === 5; // true
bst.getDepth(6) === 3; // true
bst.getLeftMost()?.key === 1; // true
bst.delete(6);
bst.get(6); // undefined
bst.isAVLBalanced(); // true
bst.bfs()[0] === 11; // true
bst.print()
// ______________11_____
// / \
// ___3_______ _13_____
// / \ / \
// 1_ _____8____ 12 _15__
// \ / \ / \
// 2 4_ _10 14 16
// \ /
// 5_ 9
// \
// 7
const objBST = new BST();
objBST.add(11, { "name": "Pablo", "size": 15 });
objBST.add(3, { "name": "Kirk", "size": 1 });
objBST.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5], [
{ "name": "Alice", "size": 15 },
{ "name": "Bob", "size": 1 },
{ "name": "Charlie", "size": 8 },
{ "name": "David", "size": 13 },
{ "name": "Emma", "size": 16 },
{ "name": "Frank", "size": 2 },
{ "name": "Grace", "size": 6 },
{ "name": "Hannah", "size": 9 },
{ "name": "Isaac", "size": 12 },
{ "name": "Jack", "size": 14 },
{ "name": "Katie", "size": 4 },
{ "name": "Liam", "size": 7 },
{ "name": "Mia", "size": 10 },
{ "name": "Noah", "size": 5 }
]
);
objBST.delete(11);
```
### AVLTree snippet
```ts
import { AVLTree } from 'data-structure-typed';
const avlTree = new AVLTree();
avlTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
avlTree.isAVLBalanced(); // true
avlTree.delete(10);
avlTree.isAVLBalanced(); // true
```
### Directed Graph simple snippet
```ts
import { DirectedGraph } from 'data-structure-typed';
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.hasVertex('A'); // true
graph.hasVertex('B'); // true
graph.hasVertex('C'); // false
graph.addEdge('A', 'B');
graph.hasEdge('A', 'B'); // true
graph.hasEdge('B', 'A'); // false
graph.deleteEdgeSrcToDest('A', 'B');
graph.hasEdge('A', 'B'); // false
graph.addVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'C');
const topologicalOrderKeys = graph.topologicalSort(); // ['A', 'B', 'C']
```
### Undirected Graph snippet
```ts
import { UndirectedGraph } from 'data-structure-typed';
const graph = new UndirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.deleteVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'D');
const dijkstraResult = graph.dijkstra('A');
Array.from(dijkstraResult?.seen ?? []).map(vertex => vertex.key) // ['A', 'B', 'D']
```
[//]: # (No deletion!!! Start of Example Replace Section)
[//]: # (No deletion!!! End of Example Replace Section)
## API docs & Examples
[API Docs](https://data-structure-typed-docs.vercel.app)
[Live Examples](https://vivid-algorithm.vercel.app)
## Benchmark
MacBook Pro (15-inch, 2018)
Processor 2.2 GHz 6-Core Intel Core i7
Memory 16 GB 2400 MHz DDR4
Graphics Radeon Pro 555X 4 GB
Intel UHD Graphics 630 1536 MB
macOS Big Sur
Version 11.7.9
***Our performance testing is conducted directly on the TypeScript source code. The actual performance of the compiled JavaScript code is generally 3 times higher. We have compared it with C++, and it is only 30% slower than C++.***
Try it [on gitpod](https://gitpod.io#snapshot/93383de4-ca4c-4854-8c80-4359e681a96f)
Just run
```shell
pnpm perf:rbtree
```
```html
1,000,000 add randomly: 1.367s
1,000,000 add: 374.859ms
1,000,000 get: 8.025ms
1,000,000 getNode: 1.293s
```
[//]: # (No deletion!!! Start of Replace Section)
heap
test nametime taken (ms)sample mean (secs)sample deviation100,000 add6.850.013.38e-4100,000 add & poll35.350.048.44e-4
avl-tree
test nametime taken (ms)sample mean (secs)sample deviation100,000 add302.890.300.01100,000 add randomly381.830.380.00100,000 get0.605.95e-42.33e-4100,000 getNode150.610.150.00100,000 iterator28.230.030.00100,000 add & delete orderly505.570.510.01100,000 add & delete randomly677.360.680.00
rb-tree
test nametime taken (ms)sample mean (secs)sample deviation100,000 add212.770.219.84e-4100,000 add randomly163.700.160.00100,000 get1.190.002.44e-4100,000 getNode347.390.350.01100,000 node mode add randomly162.260.160.00100,000 node mode get344.900.340.00100,000 iterator27.480.030.00100,000 add & delete orderly386.330.390.00100,000 add & delete randomly520.660.520.00
doubly-linked-list
test nametime taken (ms)sample mean (secs)sample deviation1,000,000 push179.280.180.021,000,000 unshift197.220.200.051,000,000 unshift & shift153.160.150.001,000,000 addBefore247.300.250.03
directed-graph
test nametime taken (ms)sample mean (secs)sample deviation1,000 addVertex0.109.92e-51.16e-61,000 addEdge6.440.010.001,000 getVertex0.109.82e-51.13e-61,000 getEdge22.600.020.00tarjan186.560.190.00topologicalSort145.420.150.01
queue
test nametime taken (ms)sample mean (secs)sample deviation1,000,000 push47.740.050.02100,000 push & shift5.390.011.25e-4Native JS Array 100,000 push & shift2225.502.230.10
deque
test nametime taken (ms)sample mean (secs)sample deviation1,000,000 push22.880.020.011,000,000 push & pop27.950.030.011,000,000 push & shift29.830.030.01100,000 push & shift2.710.009.03e-4Native JS Array 100,000 push & shift2182.032.180.04100,000 unshift & shift2.610.008.71e-4Native JS Array 100,000 unshift & shift4185.904.190.04
hash-map
test nametime taken (ms)sample mean (secs)sample deviation1,000,000 set253.450.250.07Native JS Map 1,000,000 set228.900.230.02Native JS Set 1,000,000 add179.650.180.011,000,000 set & get234.960.230.06Native JS Map 1,000,000 set & get284.900.280.01Native JS Set 1,000,000 add & has254.900.250.031,000,000 ObjKey set & get403.740.400.10Native JS Map 1,000,000 ObjKey set & get340.180.340.07Native JS Set 1,000,000 ObjKey add & has300.250.300.06
trie
test nametime taken (ms)sample mean (secs)sample deviation100,000 push44.110.048.55e-4100,000 getWords86.670.090.00
stack
test nametime taken (ms)sample mean (secs)sample deviation1,000,000 push43.180.040.011,000,000 push & pop48.400.050.02
[//]: # (No deletion!!! End of Replace Section)
## The corresponding relationships between data structures in different language standard libraries.
Data Structure Typed
C++ STL
java.util
Python collections
Heap<E>
-
-
heapq
PriorityQueue<E>
priority_queue<T>
PriorityQueue<E>
-
Deque<E>
deque<T>
ArrayDeque<E>
deque
Queue<E>
queue<T>
Queue<E>
-
HashMap<K, V>
unordered_map<K, V>
HashMap<K, V>
defaultdict
DoublyLinkedList<E>
list<T>
LinkedList<E>
-
SinglyLinkedList<E>
-
-
-
BinaryTree<K, V>
-
-
-
BST<K, V>
-
-
-
RedBlackTree<E>
set<T>
TreeSet<E>
-
RedBlackTree<K, V>
map<K, V>
TreeMap<K, V>
-
TreeMultiMap<K, V>
multimap<K, V>
-
-
TreeMultiMap<E>
multiset<T>
-
-
Trie
-
-
-
DirectedGraph<V, E>
-
-
-
UndirectedGraph<V, E>
-
-
-
PriorityQueue<E>
priority_queue<T>
PriorityQueue<E>
-
Array<E>
vector<T>
ArrayList<E>
list
Stack<E>
stack<T>
Stack<E>
-
HashMap<E>
unordered_set<T>
HashSet<E>
set
-
unordered_multiset
-
Counter
ES6 Map<K, V>
-
LinkedHashMap<K, V>
OrderedDict
-
unordered_multimap<K, V>
-
-
-
bitset<N>
-
-
## Built-in classic algorithms
Algorithm
Function Description
Iteration Type
Binary Tree DFS
Traverse a binary tree in a depth-first manner, starting from the root node, first visiting the left subtree,
and then the right subtree, using recursion.
Recursion + Iteration
Binary Tree BFS
Traverse a binary tree in a breadth-first manner, starting from the root node, visiting nodes level by level
from left to right.
Iteration
Graph DFS
Traverse a graph in a depth-first manner, starting from a given node, exploring along one path as deeply as
possible, and backtracking to explore other paths. Used for finding connected components, paths, etc.
Recursion + Iteration
Binary Tree Morris
Morris traversal is an in-order traversal algorithm for binary trees with O(1) space complexity. It allows tree
traversal without additional stack or recursion.
Iteration
Graph BFS
Traverse a graph in a breadth-first manner, starting from a given node, first visiting nodes directly connected
to the starting node, and then expanding level by level. Used for finding shortest paths, etc.
Recursion + Iteration
Graph Tarjan's Algorithm
Find strongly connected components in a graph, typically implemented using depth-first search.
Recursion
Graph Bellman-Ford Algorithm
Finding the shortest paths from a single source, can handle negative weight edges
Iteration
Graph Dijkstra's Algorithm
Finding the shortest paths from a single source, cannot handle negative weight edges
Iteration
Graph Floyd-Warshall Algorithm
Finding the shortest paths between all pairs of nodes
Iteration
Graph getCycles
Find all cycles in a graph or detect the presence of cycles.
Recursion
Graph getCutVertices
Find cut vertices in a graph, which are nodes that, when removed, increase the number of connected components in
the graph.
Recursion
Graph getSCCs
Find strongly connected components in a graph, which are subgraphs where any two nodes can reach each other.
Recursion
Graph getBridges
Find bridges in a graph, which are edges that, when removed, increase the number of connected components in the
graph.
Recursion
Graph topologicalSort
Perform topological sorting on a directed acyclic graph (DAG) to find a linear order of nodes such that all
directed edges go from earlier nodes to later nodes.
Recursion
## Software Engineering Design Standards
We strictly adhere to computer science theory and software development standards. Our LinkedList is designed in the
traditional sense of the LinkedList data structure, and we refrain from substituting it with a Deque solely for the
purpose of showcasing performance test data. However, we have also implemented a Deque based on a dynamic array
concurrently.
Principle
Description
Practicality
Follows ES6 and ESNext standards, offering unified and considerate optional parameters, and simplifies method names.
Extensibility
Adheres to OOP (Object-Oriented Programming) principles, allowing inheritance for all data structures.
Modularization
Includes data structure modularization and independent NPM packages.
Efficiency
All methods provide time and space complexity, comparable to native JS performance.
Maintainability
Follows open-source community development standards, complete documentation, continuous integration, and adheres to TDD (Test-Driven Development) patterns.
Testability
Automated and customized unit testing, performance testing, and integration testing.
Portability
Plans for porting to Java, Python, and C++, currently achieved to 80%.
Reusability
Fully decoupled, minimized side effects, and adheres to OOP.
Security
Carefully designed security for member variables and methods. Read-write separation. Data structure software does not need to consider other security aspects.
Scalability
Data structure software does not involve load issues.
## supported module system
Now you can use it in Node.js and browser environments
CommonJS:**`require export.modules =`**
ESModule: **`import export`**
Typescript: **`import export`**
UMD: **`var Deque = dataStructureTyped.Deque`**
### CDN
Copy the line below into the head tag in an HTML document.
#### development
```html
```
#### production
```html
```
Copy the code below into the script tag of your HTML, and you're good to go with your development.
```js
const { Heap } = dataStructureTyped;
const {
BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultiMap,
DirectedVertex, AVLTreeNode
} = dataStructureTyped;
```
