https://github.com/MinghuiChen43/awesome-deep-phenomena
A curated list of papers of interesting empirical study and insight on deep learning. Continually updating...
https://github.com/MinghuiChen43/awesome-deep-phenomena
List: awesome-deep-phenomena
awesome-list deep-learning-theory double-descent emergence empirical-research grokking information-bottleneck-theory lottery-ticket-hypothesis neural-collapse neural-tangent-kernel neuroscience-inspired-ai non-convex-optimization phase-transitions
Last synced: 3 months ago
JSON representation
A curated list of papers of interesting empirical study and insight on deep learning. Continually updating...
- Host: GitHub
- URL: https://github.com/MinghuiChen43/awesome-deep-phenomena
- Owner: MinghuiChen43
- License: mit
- Created: 2020-06-23T11:43:04.000Z (almost 5 years ago)
- Default Branch: master
- Last Pushed: 2024-05-17T06:38:50.000Z (about 1 year ago)
- Last Synced: 2024-05-21T01:44:29.544Z (about 1 year ago)
- Topics: awesome-list, deep-learning-theory, double-descent, emergence, empirical-research, grokking, information-bottleneck-theory, lottery-ticket-hypothesis, neural-collapse, neural-tangent-kernel, neuroscience-inspired-ai, non-convex-optimization, phase-transitions
- Homepage:
- Size: 19.2 MB
- Stars: 213
- Watchers: 22
- Forks: 8
- Open Issues: 0
-
Metadata Files:
- Readme: README.md
- License: LICENSE
Awesome Lists containing this project
- awesome-trustworthy-deep-learning - Awesome Deep Phenomena - deep-phenomena)  (Other Lists)
- ultimate-awesome - awesome-deep-phenomena - A curated list of papers of interesting empirical study and insight on deep learning. Continually updating. (Other Lists / Julia Lists)
README
[](https://github.com/MinghuiChen43/awesome-deep-phenomena/graphs/commit-activity)


[](https://github.com/MinghuiChen43/awesome-deep-phenomena/stargazers)
[](https://github.com/MinghuiChen43/awesome-deep-phenomena)
[](https://github.com/MinghuiChen43/awesome-deep-phenomena/watchers)
[](https://github.com/MinghuiChen43/awesome-deep-phenomena/network/members)
# Awesome Deep Phenomena [](https://github.com/sindresorhus/awesome)
Our understanding of modern neural networks lags behind their practical successes. This growing gap poses a challenge to the pace of progress in machine learning because fewer pillars of knowledge are available to designers of models and algorithms [(Hanie Sedghi)](https://odsc.com/speakers/understanding-deep-learning-phenomena/). Inspired by the [ICML 2019 workshop Identifying and Understanding Deep Learning Phenomena](http://deep-phenomena.org/), I collect papers and related resources which present interesting empirical study and insight into the nature of deep learning.
# Table of Contents

- [Empirical Study](#empirical-study)
- [Neural Collapse](#neural-collapse)
- [Deep Double Descent](#deep-double-descent)
- [Lottery Ticket Hypothesis](#lottery-ticket-hypothesis)
- [Emergence and Phase Transitions](#emergence-and-phase-transitions)
- [Interactions with Neuroscience](#interactions-with-neuroscience)
- [Information Bottleneck](#information-bottleneck)
- [Neural Tangent Kernel](#neural-tangent-kernel)
- [Other Papers](#others)
- [Resources](#related-resources)
## Empirical Study

### Empirical Study: 2024
- Rethinking Conventional Wisdom in Machine Learning: From Generalization to Scaling. [[paper]](https://arxiv.org/abs/2409.15156)
- Lechao Xiao.
- Key Word: Regularization; Generalization; Neural Scaling Law.
- Digest This paper explores the shift in machine learning from focusing on minimizing generalization error to reducing approximation error, particularly in the context of large language models (LLMs) and scaling laws. It questions whether traditional regularization principles, like L2 regularization and small batch sizes, remain relevant in this new paradigm. The authors introduce the concept of “scaling law crossover,” where techniques effective at smaller scales may fail as model size increases. The paper raises two key questions: what new principles should guide model scaling, and how can models be effectively compared at large scales where only single experiments are feasible?
- AI models collapse when trained on recursively generated data. [[paper]](https://www.nature.com/articles/s41586-024-07566-y?utm_medium=Social&utm_campaign=nature&utm_source=Twitter#Echobox=1721898113)
- Ilia Shumailov, Zakhar Shumaylov, Yiren Zhao, Nicolas Papernot, Ross Anderson, Yarin Gal. *Nature*
- Key Word: Model Collapse; Generative Model.
- Digest The paper demonstrates that AI models trained on recursively generated data suffer from a collapse in performance. This finding highlights the critical need for diverse and high-quality data sources to maintain the robustness and reliability of AI systems.
- Not All Language Model Features Are Linear. [[paper]](https://arxiv.org/abs/2405.14860)
- Joshua Engels, Isaac Liao, Eric J. Michaud, Wes Gurnee, Max Tegmark.
- Key Word: Large Language Model; Linear Representation Hypothesis.
- Digest This paper challenges the linear representation hypothesis in language models by proposing that some representations are inherently multi-dimensional. Using sparse autoencoders, the authors identify interpretable multi-dimensional features in GPT-2 and Mistral 7B, such as circular features for days and months, and demonstrate their computational significance through intervention experiments.
- LoRA Learns Less and Forgets Less. [[paper]](https://arxiv.org/abs/2405.09673)
- Dan Biderman, Jose Gonzalez Ortiz, Jacob Portes, Mansheej Paul, Philip Greengard, Connor Jennings, Daniel King, Sam Havens, Vitaliy Chiley, Jonathan Frankle, Cody Blakeney, John P. Cunningham.
- Key Word: LoRA; Fine-Tuning; Learning-Forgetting Trade-off.
- Digest The study compares the performance of Low-Rank Adaptation (LoRA), a parameter-efficient finetuning method for large language models, with full finetuning in programming and mathematics domains. While LoRA generally underperforms compared to full finetuning, it better maintains the base model's performance on tasks outside the target domain, providing stronger regularization than common techniques like weight decay and dropout. Full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, which may explain some performance gaps. The study concludes with best practices for finetuning with LoRA.
- The Platonic Representation Hypothesis. [[paper]](https://arxiv.org/abs/2405.07987)
- Minyoung Huh, Brian Cheung, Tongzhou Wang, Phillip Isola.
- Key Word: Foundation Models; Representational Convergence.
- Digest The paper argues that representations in AI models, especially deep networks, are converging. This convergence is observed across time, multiple domains, and different data modalities. As models get larger, they measure distance between data points in increasingly similar ways. The authors hypothesize that this convergence is moving towards a shared statistical model of reality, which they term the "platonic representation." They discuss potential selective pressures towards this representation and explore the implications, limitations, and counterexamples to their analysis.
- The Unreasonable Ineffectiveness of the Deeper Layers. [[paper]](https://arxiv.org/abs/2403.17887)
- Andrey Gromov, Kushal Tirumala, Hassan Shapourian, Paolo Glorioso, Daniel A. Roberts.
- Key Word: Large Language Model; Pruning.
- Digest This study explores a straightforward layer-pruning approach on widely-used pretrained large language models (LLMs), showing that removing up to half of the layers results in only minimal performance decline on various question-answering benchmarks. The method involves selecting the best layers to prune based on layer similarity, followed by minimal finetuning to mitigate any loss in performance. Specifically, it employs parameter-efficient finetuning techniques like quantization and Low Rank Adapters (QLoRA), enabling experiments on a single A100 GPU. The findings indicate that layer pruning could both reduce finetuning computational demands and enhance inference speed and memory efficiency. Moreover, the resilience of LLMs to layer removal raises questions about the effectiveness of current pretraining approaches or highlights the significant knowledge-storing capacity of the models' shallower layers.
- Unfamiliar Finetuning Examples Control How Language Models Hallucinate. [[paper]](https://arxiv.org/abs/2403.05612)
- Katie Kang, Eric Wallace, Claire Tomlin, Aviral Kumar, Sergey Levine.
- Key Word: Large Language Model; Hallucination; Supervised Fine-Tuning.
- Digest This study investigates the propensity of large language models (LLMs) to produce plausible but factually incorrect responses, focusing on their behavior with unfamiliar concepts. The research identifies a pattern where LLMs resort to hedged predictions for unfamiliar inputs, influenced by the supervision of such examples during fine-tuning. By adjusting the supervision of these examples, it's possible to direct LLM responses towards acknowledging their uncertainty (e.g., by saying "I don't know").
- When Scaling Meets LLM Finetuning: The Effect of Data, Model and Finetuning Method. [[paper]](https://arxiv.org/abs/2402.17193)
- Biao Zhang, Zhongtao Liu, Colin Cherry, Orhan Firat.
- Key Word: Neural Scaling Laws; Large Language Model; Fine-Tuning.
- Digest This study investigates how scaling factors—model size, pretraining data size, finetuning parameter size, and finetuning data size—affect finetuning performance of large language models (LLMs) across two methods: full-model tuning (FMT) and parameter efficient tuning (PET). Experiments on bilingual LLMs for translation and summarization tasks reveal that finetuning performance scales multiplicatively with data size and other factors, favoring model scaling over pretraining data scaling, with PET parameter scaling showing limited effectiveness. These insights suggest the choice of finetuning method is highly task- and data-dependent, offering guidance for optimizing LLM finetuning strategies.
- Rethink Model Re-Basin and the Linear Mode Connectivity. [[paper]](https://arxiv.org/abs/2402.05966)
- Xingyu Qu, Samuel Horvath.
- Key Word: Linear Mode Connectivity; Model Merging; Re-Normalization; Pruning.
- Digest The paper discusses the "model re-basin regime," where most solutions found by stochastic gradient descent (SGD) in sufficiently wide models converge to similar states, impacting model averaging. It identifies limitations in current strategies due to a poor understanding of the mechanisms involved. The study critiques existing matching algorithms for their inadequacies and proposes that proper re-normalization can address these issues. By adopting a more analytical approach, the paper reveals how matching algorithms and re-normalization interact, offering clearer insights and improvements over previous work. This includes a connection between linear mode connectivity and pruning, leading to a new lightweight post-pruning method that enhances existing pruning techniques.
- How Good is a Single Basin? [[paper]](https://arxiv.org/abs/2402.03187)
- Kai Lion, Lorenzo Noci, Thomas Hofmann, Gregor Bachmann.
- Key Word: Linear Mode Connectivity; Deep Ensembles.
- Digest This paper investigates the assumption that the multi-modal nature of neural loss landscapes is key to the success of deep ensembles. By creating "connected" ensembles that are confined to a single basin, the study finds that this limitation indeed reduces performance. However, it also discovers that distilling knowledge from multiple basins into these connected ensembles can offset the performance deficit, effectively creating multi-basin deep ensembles within a single basin. This suggests that while knowledge from outside a given basin exists within it, it is not readily accessible without learning from other basins.
### Empirical Study: 2023
- Truth is in There: Improving Reasoning in Language Models with Layer-Selective Rank Reduction. [[paper]](https://arxiv.org/abs/2312.13558) [[code]](https://github.com/pratyushasharma/laser)
- Pratyusha Sharma, Jordan T. Ash, Dipendra Misra
- Key Word: Large Language Models; Reasoning.
- Digest Transformer-based Large Language Models (LLMs) have become a fixture in modern machine learning. Correspondingly, significant resources are allocated towards research that aims to further advance this technology, typically resulting in models of increasing size that are trained on increasing amounts of data. This work, however, demonstrates the surprising result that it is often possible to significantly improve the performance of LLMs by selectively removing higher-order components of their weight matrices. This simple intervention, which we call LAyer-SElective Rank reduction (LASER), can be done on a model after training has completed, and requires no additional parameters or data. We show extensive experiments demonstrating the generality of this finding across language models and datasets, and provide in-depth analyses offering insights into both when LASER is effective and the mechanism by which it operates.
- The Transient Nature of Emergent In-Context Learning in Transformers. [[paper]](https://arxiv.org/abs/2311.08360)
- Aaditya K. Singh, Stephanie C.Y. Chan, Ted Moskovitz, Erin Grant, Andrew M. Saxe, Felix Hill. *NeurIPS 2023*
- Key Word: In-Context Learning.
- Digest This paper shows that in-context learning (ICL) in transformers, where models exhibit abilities not explicitly trained for, is often transient rather than persistent during training. The authors find ICL emerges then disappears, giving way to in-weights learning (IWL). This occurs across model sizes and datasets, raising questions around stopping training early for ICL vs later for IWL. They suggest L2 regularization may lead to more persistent ICL, removing the need for early stopping based on ICL validation. The transience may be caused by competition between emerging ICL and IWL circuits in the model.
- What do larger image classifiers memorise? [[paper]](https://arxiv.org/abs/2310.05337)
- Michal Lukasik, Vaishnavh Nagarajan, Ankit Singh Rawat, Aditya Krishna Menon, Sanjiv Kumar.
- Key Word: Large Model; Memorization.
- Digest This paper explores the relationship between memorization and generalization in modern neural networks. It discusses Feldman's metric for measuring memorization and applies it to ResNet models for image classification. The paper then investigates whether larger neural models memorize more and finds that memorization trajectories vary across different training examples and model sizes. Additionally, it notes that knowledge distillation, a model compression technique, tends to inhibit memorization while improving generalization, particularly on examples with increasing memorization trajectories.
- Can Neural Network Memorization Be Localized? [[paper]](https://arxiv.org/abs/2307.09542)
- Pratyush Maini, Michael C. Mozer, Hanie Sedghi, Zachary C. Lipton, J. Zico Kolter, Chiyuan Zhang. *ICML 2023*
- Key Word: Atypical Example Memorization; Location of Memorization; Task Specific Neurons.
- Digest The paper demonstrates that memorization in deep overparametrized networks is not limited to individual layers but rather confined to a small set of neurons across various layers of the model. Through experimental evidence from gradient accounting, layer rewinding, and retraining, the study reveals that most layers are redundant for example memorization, and the contributing layers are typically not the final layers. Additionally, the authors propose a new form of dropout called example-tied dropout, which allows them to selectively direct memorization to a pre-defined set of neurons, effectively reducing memorization accuracy while also reducing the generalization gap.
- No Wrong Turns: The Simple Geometry Of Neural Networks Optimization Paths. [[paper]](https://arxiv.org/abs/2306.11922)
- Charles Guille-Escuret, Hiroki Naganuma, Kilian Fatras, Ioannis Mitliagkas.
- Key Word: Restricted Secant Inequality; Error Bound; Loss Landscape Geometry.
- Digest The paper explores the geometric properties of optimization paths in neural networks and reveals that the quantities related to the restricted secant inequality and error bound exhibit consistent behavior during training, suggesting that optimization trajectories encounter no significant obstacles and maintain stable dynamics, leading to linear convergence and supporting commonly used learning rate schedules.
- Sharpness-Aware Minimization Leads to Low-Rank Features. [[paper]](https://arxiv.org/abs/2305.16292)
- Maksym Andriushchenko, Dara Bahri, Hossein Mobahi, Nicolas Flammarion.
- Key Word: Sharpness-Aware Minimization; Low-Rank Features.
- Digest Sharpness-aware minimization (SAM) is a method that minimizes the sharpness of the training loss of a neural network. It improves generalization and reduces the feature rank at different layers of a neural network. This low-rank effect occurs for different architectures and objectives. A significant number of activations get pruned by SAM, contributing to rank reduction. This effect can also occur in deep networks.
- A surprisingly simple technique to control the pretraining bias for better transfer: Expand or Narrow your representation. [[paper]](https://arxiv.org/abs/2304.05369)
- Florian Bordes, Samuel Lavoie, Randall Balestriero, Nicolas Ballas, Pascal Vincent.
- Key Word: Pretraining; Fine-Tuning; Information Bottleneck.
- Digest A commonly used trick in SSL, shown to make deep networks more robust to such bias, is the addition of a small projector (usually a 2 or 3 layer multi-layer perceptron) on top of a backbone network during training. In contrast to previous work that studied the impact of the projector architecture, we here focus on a simpler, yet overlooked lever to control the information in the backbone representation. We show that merely changing its dimensionality -- by changing only the size of the backbone's very last block -- is a remarkably effective technique to mitigate the pretraining bias.
- Why is the winner the best? [[paper]](https://arxiv.org/abs/2303.17719)
- Author List Matthias Eisenmann, Annika Reinke, Vivienn Weru, Minu Dietlinde Tizabi, Fabian Isensee, Tim J. Adler, Sharib Ali, Vincent Andrearczyk, Marc Aubreville, Ujjwal Baid, Spyridon Bakas, Niranjan Balu, Sophia Bano, Jorge Bernal, Sebastian Bodenstedt, Alessandro Casella, Veronika Cheplygina, Marie Daum, Marleen de Bruijne, Adrien Depeursinge, Reuben Dorent, Jan Egger, David G. Ellis, Sandy Engelhardt, Melanie Ganz, Noha Ghatwary, Gabriel Girard, Patrick Godau, Anubha Gupta, Lasse Hansen, Kanako Harada, Mattias Heinrich, Nicholas Heller, Alessa Hering, Arnaud Huaulmé, Pierre Jannin, Ali Emre Kavur, Oldřich Kodym, Michal Kozubek, Jianning Li, Hongwei Li, Jun Ma, Carlos Martín-Isla, Bjoern Menze, Alison Noble, Valentin Oreiller, Nicolas Padoy, Sarthak Pati, Kelly Payette, Tim Rädsch, Jonathan Rafael-Patiño, Vivek Singh Bawa, Stefanie Speidel, Carole H. Sudre, Kimberlin van Wijnen, Martin Wagner, Donglai Wei, Amine Yamlahi, Moi Hoon Yap, Chun Yuan, Maximilian Zenk, Aneeq Zia, David Zimmerer, Dogu Baran Aydogan, Binod Bhattarai, Louise Bloch, Raphael Brüngel, Jihoon Cho, Chanyeol Choi, Qi Dou, Ivan Ezhov, Christoph M. Friedrich, Clifton Fuller, Rebati Raman Gaire, Adrian Galdran, Álvaro García Faura, Maria Grammatikopoulou, SeulGi Hong, Mostafa Jahanifar, Ikbeom Jang, Abdolrahim Kadkhodamohammadi, Inha Kang, Florian Kofler, Satoshi Kondo, Hugo Kuijf, Mingxing Li, Minh Huan Luu, Tomaž Martinčič, Pedro Morais, Mohamed A. Naser, Bruno Oliveira, David Owen, Subeen Pang, Jinah Park, Sung-Hong Park, Szymon Płotka, Elodie Puybareau, Nasir Rajpoot, Kanghyun Ryu, Numan Saeed , Adam Shephard, Pengcheng Shi, Dejan Štepec, Ronast Subedi, Guillaume Tochon, Helena R. Torres, Helene Urien, João L. Vilaça, Kareem Abdul Wahid, Haojie Wang, Jiacheng Wang, Liansheng Wang, Xiyue Wang, Benedikt Wiestler, Marek Wodzinski, Fangfang Xia, Juanying Xie, Zhiwei Xiong, Sen Yang, Yanwu Yang, Zixuan Zhao, Klaus Maier-Hein, Paul F. Jäger, Annette Kopp-Schneider, Lena Maier-Hein.
- Key Word: Benchmarking Competitions; Medical Imaging.
- Digest The article discusses the lack of investigation into what can be learned from international benchmarking competitions for image analysis methods. The authors conducted a multi-center study of 80 competitions conducted in the scope of IEEE ISBI 2021 and MICCAI 2021 to address this gap. Based on comprehensive descriptions of the submitted algorithms and their rankings, as well as participation strategies, statistical analyses revealed common characteristics of winning solutions. These typically include the use of multi-task learning and/or multi-stage pipelines, a focus on augmentation, image preprocessing, data curation, and postprocessing.
- Sparks of Artificial General Intelligence: Early experiments with GPT-4. [[paper]](https://arxiv.org/abs/2303.12712)
- Sébastien Bubeck, Varun Chandrasekaran, Ronen Eldan, Johannes Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, Yuanzhi Li, Scott Lundberg, Harsha Nori, Hamid Palangi, Marco Tulio Ribeiro, Yi Zhang.
- Key Word: Artificial General Intelligence; Benchmarking; GPT.
- Digest We discuss the rising capabilities and implications of these models. We demonstrate that, beyond its mastery of language, GPT-4 can solve novel and difficult tasks that span mathematics, coding, vision, medicine, law, psychology and more, without needing any special prompting. Moreover, in all of these tasks, GPT-4's performance is strikingly close to human-level performance, and often vastly surpasses prior models such as ChatGPT.
- Is forgetting less a good inductive bias for forward transfer? [[paper]](https://arxiv.org/abs/2303.08207)
- Jiefeng Chen, Timothy Nguyen, Dilan Gorur, Arslan Chaudhry. *ICLR 2023*
- Key Word: Continual Learning; Catastrophic Forgetting; Forward Transfer; Inductive Bias.
- Digest One of the main motivations of studying continual learning is that the problem setting allows a model to accrue knowledge from past tasks to learn new tasks more efficiently. However, recent studies suggest that the key metric that continual learning algorithms optimize, reduction in catastrophic forgetting, does not correlate well with the forward transfer of knowledge. We believe that the conclusion previous works reached is due to the way they measure forward transfer. We argue that the measure of forward transfer to a task should not be affected by the restrictions placed on the continual learner in order to preserve knowledge of previous tasks.
- Dropout Reduces Underfitting. [[paper]](https://arxiv.org/abs/2303.01500) [[code]](https://github.com/facebookresearch/dropout)
- Zhuang Liu, Zhiqiu Xu, Joseph Jin, Zhiqiang Shen, Trevor Darrell.
- Key Word: Dropout; Overfitting.
- Digest In this study, we demonstrate that dropout can also mitigate underfitting when used at the start of training. During the early phase, we find dropout reduces the directional variance of gradients across mini-batches and helps align the mini-batch gradients with the entire dataset's gradient. This helps counteract the stochasticity of SGD and limit the influence of individual batches on model training.
- The Role of Pre-training Data in Transfer Learning. [[paper]](https://arxiv.org/abs/2302.13464)
- Rahim Entezari, Mitchell Wortsman, Olga Saukh, M.Moein Shariatnia, Hanie Sedghi, Ludwig Schmidt.
- Key Word: Pre-training; Transfer Learning.
- Digest We investigate the impact of pre-training data distribution on the few-shot and full fine-tuning performance using 3 pre-training methods (supervised, contrastive language-image and image-image), 7 pre-training datasets, and 9 downstream datasets. Through extensive controlled experiments, we find that the choice of the pre-training data source is essential for the few-shot transfer, but its role decreases as more data is made available for fine-tuning.
- The Dormant Neuron Phenomenon in Deep Reinforcement Learning. [[paper]](https://arxiv.org/abs/2302.12902) [[code]](https://github.com/google/dopamine)
- Ghada Sokar, Rishabh Agarwal, Pablo Samuel Castro, Utku Evci.
- Key Word: Dormant Neuron; Deep Reinforcement Learning.
- Digest The paper identifies the dormant neuron phenomenon in deep reinforcement learning, where inactive neurons increase and hinder network expressivity, affecting learning. To address this, they propose a method called ReDo, which recycles dormant neurons during training. ReDo reduces the number of dormant neurons, maintains network expressiveness, and leads to improved performance.
- Cliff-Learning. [[paper]](https://arxiv.org/abs/2302.07348)
- Tony T. Wang, Igor Zablotchi, Nir Shavit, Jonathan S. Rosenfeld.
- Key Word: Foundation Models; Fine-Tuning.
- Digest We study the data-scaling of transfer learning from foundation models in the low-downstream-data regime. We observe an intriguing phenomenon which we call cliff-learning. Cliff-learning refers to regions of data-scaling laws where performance improves at a faster than power law rate (i.e. regions of concavity on a log-log scaling plot).
### Empirical Study: 2022
- ModelDiff: A Framework for Comparing Learning Algorithms. [[paper]](https://arxiv.org/abs/2211.12491) [[code]](https://github.com/MadryLab/modeldiff)
- Harshay Shah, Sung Min Park, Andrew Ilyas, Aleksander Madry.
- Key Word: Representation-based Comparison; Example-level Comparisons; Comparing Feature Attributions.
- Digest We study the problem of (learning) algorithm comparison, where the goal is to find differences between models trained with two different learning algorithms. We begin by formalizing this goal as one of finding distinguishing feature transformations, i.e., input transformations that change the predictions of models trained with one learning algorithm but not the other. We then present ModelDiff, a method that leverages the datamodels framework (Ilyas et al., 2022) to compare learning algorithms based on how they use their training data.
- Overfreezing Meets Overparameterization: A Double Descent Perspective on Transfer Learning of Deep Neural Networks. [[paper]](https://arxiv.org/abs/2211.11074)
- Yehuda Dar, Lorenzo Luzi, Richard G. Baraniuk.
- Key Word: Transfer Learning; Deep Double Descent; Overfreezing.
- Digest We study the generalization behavior of transfer learning of deep neural networks (DNNs). We adopt the overparameterization perspective -- featuring interpolation of the training data (i.e., approximately zero train error) and the double descent phenomenon -- to explain the delicate effect of the transfer learning setting on generalization performance. We study how the generalization behavior of transfer learning is affected by the dataset size in the source and target tasks, the number of transferred layers that are kept frozen in the target DNN training, and the similarity between the source and target tasks.
- How to Fine-Tune Vision Models with SGD. [[paper]](https://arxiv.org/abs/2211.09359)
- Ananya Kumar, Ruoqi Shen, Sébastien Bubeck, Suriya Gunasekar.
- Key Word: Fine-Tuning; Out-of-Distribution Generalization.
- Digest We show that fine-tuning with AdamW performs substantially better than SGD on modern Vision Transformer and ConvNeXt models. We find that large gaps in performance between SGD and AdamW occur when the fine-tuning gradients in the first "embedding" layer are much larger than in the rest of the model. Our analysis suggests an easy fix that works consistently across datasets and models: merely freezing the embedding layer (less than 1\% of the parameters) leads to SGD performing competitively with AdamW while using less memory.
- What Images are More Memorable to Machines? [[paper]](https://arxiv.org/abs/2211.07625) [[code]](https://github.com/JunlinHan/MachineMem)
- Junlin Han, Huangying Zhan, Jie Hong, Pengfei Fang, Hongdong Li, Lars Petersson, Ian Reid.
- Key Word: Self-Supervised Memorization Quantification.
- Digest This paper studies the problem of measuring and predicting how memorable an image is to pattern recognition machines, as a path to explore machine intelligence. Firstly, we propose a self-supervised machine memory quantification pipeline, dubbed ``MachineMem measurer'', to collect machine memorability scores of images. Similar to humans, machines also tend to memorize certain kinds of images, whereas the types of images that machines and humans memorialize are different.
- Harmonizing the object recognition strategies of deep neural networks with humans. [[paper]](https://arxiv.org/abs/2211.04533) [[code]](https://serre-lab.github.io/Harmonization/)
- Thomas Fel, Ivan Felipe, Drew Linsley, Thomas Serre.
- Key Word: Interpretation; Neural Harmonizer; Psychophysics.
- Digest Across 84 different DNNs trained on ImageNet and three independent datasets measuring the where and the how of human visual strategies for object recognition on those images, we find a systematic trade-off between DNN categorization accuracy and alignment with human visual strategies for object recognition. State-of-the-art DNNs are progressively becoming less aligned with humans as their accuracy improves. We rectify this growing issue with our neural harmonizer: a general-purpose training routine that both aligns DNN and human visual strategies and improves categorization accuracy.
- Pruning's Effect on Generalization Through the Lens of Training and Regularization. [[paper]](https://arxiv.org/abs/2210.13738)
- Tian Jin, Michael Carbin, Daniel M. Roy, Jonathan Frankle, Gintare Karolina Dziugaite.
- Key Word: Pruning; Regularization.
- Digest We show that size reduction cannot fully account for the generalization-improving effect of standard pruning algorithms. Instead, we find that pruning leads to better training at specific sparsities, improving the training loss over the dense model. We find that pruning also leads to additional regularization at other sparsities, reducing the accuracy degradation due to noisy examples over the dense model. Pruning extends model training time and reduces model size. These two factors improve training and add regularization respectively. We empirically demonstrate that both factors are essential to fully explaining pruning's impact on generalization.
- What does a deep neural network confidently perceive? The effective dimension of high certainty class manifolds and their low confidence boundaries. [[paper]](https://arxiv.org/abs/2210.05546) [[code]](https://github.com/stanislavfort/slice-dice-optimize/)
- Stanislav Fort, Ekin Dogus Cubuk, Surya Ganguli, Samuel S. Schoenholz.
- Key Word: Class Manifold; Linear Region; Out-of-Distribution Generalization.
- Digest Deep neural network classifiers partition input space into high confidence regions for each class. The geometry of these class manifolds (CMs) is widely studied and intimately related to model performance; for example, the margin depends on CM boundaries. We exploit the notions of Gaussian width and Gordon's escape theorem to tractably estimate the effective dimension of CMs and their boundaries through tomographic intersections with random affine subspaces of varying dimension. We show several connections between the dimension of CMs, generalization, and robustness.
- In What Ways Are Deep Neural Networks Invariant and How Should We Measure This? [[paper]](https://arxiv.org/abs/2210.03773)
- Henry Kvinge, Tegan H. Emerson, Grayson Jorgenson, Scott Vasquez, Timothy Doster, Jesse D. Lew. *NeurIPS 2022*
- Key Word: Invariance and Equivariance.
- Digest We explore the nature of invariance and equivariance of deep learning models with the goal of better understanding the ways in which they actually capture these concepts on a formal level. We introduce a family of invariance and equivariance metrics that allows us to quantify these properties in a way that disentangles them from other metrics such as loss or accuracy.
- Relative representations enable zero-shot latent space communication. [[paper]](https://arxiv.org/abs/2209.15430)
- Luca Moschella, Valentino Maiorca, Marco Fumero, Antonio Norelli, Francesco Locatello, Emanuele Rodolà.
- Key Word: Representation Similarity; Model stitching.
- Digest Neural networks embed the geometric structure of a data manifold lying in a high-dimensional space into latent representations. Ideally, the distribution of the data points in the latent space should depend only on the task, the data, the loss, and other architecture-specific constraints. However, factors such as the random weights initialization, training hyperparameters, or other sources of randomness in the training phase may induce incoherent latent spaces that hinder any form of reuse. Nevertheless, we empirically observe that, under the same data and modeling choices, distinct latent spaces typically differ by an unknown quasi-isometric transformation: that is, in each space, the distances between the encodings do not change. In this work, we propose to adopt pairwise similarities as an alternative data representation, that can be used to enforce the desired invariance without any additional training.
- Minimalistic Unsupervised Learning with the Sparse Manifold Transform. [[paper]](https://arxiv.org/abs/2209.15261)
- Yubei Chen, Zeyu Yun, Yi Ma, Bruno Olshausen, Yann LeCun.
- Key Word: Self-Supervision; Sparse Manifold Transform.
- Digest We describe a minimalistic and interpretable method for unsupervised learning, without resorting to data augmentation, hyperparameter tuning, or other engineering designs, that achieves performance close to the SOTA SSL methods. Our approach leverages the sparse manifold transform, which unifies sparse coding, manifold learning, and slow feature analysis. With a one-layer deterministic sparse manifold transform, one can achieve 99.3% KNN top-1 accuracy on MNIST, 81.1% KNN top-1 accuracy on CIFAR-10 and 53.2% on CIFAR-100.
- A Review of Sparse Expert Models in Deep Learning. [[paper]](https://arxiv.org/abs/2209.01667)
- William Fedus, Jeff Dean, Barret Zoph.
- Key Word: Mixture-of-Experts.
- Digest Sparse expert models are a thirty-year old concept re-emerging as a popular architecture in deep learning. This class of architecture encompasses Mixture-of-Experts, Switch Transformers, Routing Networks, BASE layers, and others, all with the unifying idea that each example is acted on by a subset of the parameters. By doing so, the degree of sparsity decouples the parameter count from the compute per example allowing for extremely large, but efficient models. The resulting models have demonstrated significant improvements across diverse domains such as natural language processing, computer vision, and speech recognition. We review the concept of sparse expert models, provide a basic description of the common algorithms, contextualize the advances in the deep learning era, and conclude by highlighting areas for future work.
- A Data-Based Perspective on Transfer Learning. [[paper]](https://arxiv.org/abs/2207.05739) [[code]](https://github.com/MadryLab/data-transfer)
- Saachi Jain, Hadi Salman, Alaa Khaddaj, Eric Wong, Sung Min Park, Aleksander Madry.
- Key Word: Transfer Learning; Influence Function; Data Leakage.
- Digest It is commonly believed that in transfer learning including more pre-training data translates into better performance. However, recent evidence suggests that removing data from the source dataset can actually help too. In this work, we take a closer look at the role of the source dataset's composition in transfer learning and present a framework for probing its impact on downstream performance. Our framework gives rise to new capabilities such as pinpointing transfer learning brittleness as well as detecting pathologies such as data-leakage and the presence of misleading examples in the source dataset.
- When Does Re-initialization Work? [[paper]](https://arxiv.org/abs/2206.10011)
- Sheheryar Zaidi, Tudor Berariu, Hyunjik Kim, Jörg Bornschein, Claudia Clopath, Yee Whye Teh, Razvan Pascanu.
- Key Word: Re-initialization; Regularization.
- Digest We conduct an extensive empirical comparison of standard training with a selection of re-initialization methods to answer this question, training over 15,000 models on a variety of image classification benchmarks. We first establish that such methods are consistently beneficial for generalization in the absence of any other regularization. However, when deployed alongside other carefully tuned regularization techniques, re-initialization methods offer little to no added benefit for generalization, although optimal generalization performance becomes less sensitive to the choice of learning rate and weight decay hyperparameters. To investigate the impact of re-initialization methods on noisy data, we also consider learning under label noise. Surprisingly, in this case, re-initialization significantly improves upon standard training, even in the presence of other carefully tuned regularization techniques.
- How You Start Matters for Generalization. [[paper]](https://arxiv.org/abs/2206.08558)
- Sameera Ramasinghe, Lachlan MacDonald, Moshiur Farazi, Hemanth Sartachandran, Simon Lucey.
- Key Word: Implicit regularization; Fourier Spectrum.
- Digest We promote a shift of focus towards initialization rather than neural architecture or (stochastic) gradient descent to explain this implicit regularization. Through a Fourier lens, we derive a general result for the spectral bias of neural networks and show that the generalization of neural networks is heavily tied to their initialization. Further, we empirically solidify the developed theoretical insights using practical, deep networks.
- Rethinking the Role of Demonstrations: What Makes In-Context Learning Work? [[paper]](https://arxiv.org/abs/2202.12837) [[code]](https://github.com/Alrope123/rethinking-demonstrations)
- Sewon Min, Xinxi Lyu, Ari Holtzman, Mikel Artetxe, Mike Lewis, Hannaneh Hajishirzi, Luke Zettlemoyer.
- Key Word: Natural Language Processing; In-Context Learning.
- Digest We show that ground truth demonstrations are in fact not required -- randomly replacing labels in the demonstrations barely hurts performance, consistently over 12 different models including GPT-3. Instead, we find that other aspects of the demonstrations are the key drivers of end task performance, including the fact that they provide a few examples of (1) the label space, (2) the distribution of the input text, and (3) the overall format of the sequence.
### Empirical Study: 2021
- Masked Autoencoders Are Scalable Vision Learners. [[paper]](https://arxiv.org/abs/2111.06377) [[code]](https://github.com/facebookresearch/mae)
- Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Dollár, Ross Girshick. *CVPR 2022*
- Key Word: Self-Supervision; Autoencoders.
- Digest This paper shows that masked autoencoders (MAE) are scalable self-supervised learners for computer vision. Our MAE approach is simple: we mask random patches of the input image and reconstruct the missing pixels. It is based on two core designs. First, we develop an asymmetric encoder-decoder architecture, with an encoder that operates only on the visible subset of patches (without mask tokens), along with a lightweight decoder that reconstructs the original image from the latent representation and mask tokens. Second, we find that masking a high proportion of the input image, e.g., 75%, yields a nontrivial and meaningful self-supervisory task.
- Learning in High Dimension Always Amounts to Extrapolation. [[paper]](https://arxiv.org/abs/2110.09485)
- Randall Balestriero, Jerome Pesenti, Yann LeCun.
- Key Word: Interpolation and Extrapolation.
- Digest The notion of interpolation and extrapolation is fundamental in various fields from deep learning to function approximation. Interpolation occurs for a sample x whenever this sample falls inside or on the boundary of the given dataset's convex hull. Extrapolation occurs when x falls outside of that convex hull. One fundamental (mis)conception is that state-of-the-art algorithms work so well because of their ability to correctly interpolate training data. A second (mis)conception is that interpolation happens throughout tasks and datasets, in fact, many intuitions and theories rely on that assumption. We empirically and theoretically argue against those two points and demonstrate that on any high-dimensional (>100) dataset, interpolation almost surely never happens.
- Understanding Dataset Difficulty with V-Usable Information. [[paper]](https://arxiv.org/abs/2110.08420) [[code]](https://github.com/kawine/dataset_difficulty)
- Kawin Ethayarajh, Yejin Choi, Swabha Swayamdipta. *ICML 2022*
- Key Word: Dataset Difficulty Measures; Information Theory.
- Digest Estimating the difficulty of a dataset typically involves comparing state-of-the-art models to humans; the bigger the performance gap, the harder the dataset is said to be. However, this comparison provides little understanding of how difficult each instance in a given distribution is, or what attributes make the dataset difficult for a given model. To address these questions, we frame dataset difficulty -- w.r.t. a model V -- as the lack of V-usable information (Xu et al., 2019), where a lower value indicates a more difficult dataset for V. We further introduce pointwise V-information (PVI) for measuring the difficulty of individual instances w.r.t. a given distribution.
- Exploring the Limits of Large Scale Pre-training. [[paper]](https://arxiv.org/abs/2110.02095)
- Samira Abnar, Mostafa Dehghani, Behnam Neyshabur, Hanie Sedghi. *ICLR 2022*
- Key Word: Pre-training.
- Digest We investigate more than 4800 experiments on Vision Transformers, MLP-Mixers and ResNets with number of parameters ranging from ten million to ten billion, trained on the largest scale of available image data (JFT, ImageNet21K) and evaluated on more than 20 downstream image recognition tasks. We propose a model for downstream performance that reflects the saturation phenomena and captures the nonlinear relationship in performance of upstream and downstream tasks.
- Stochastic Training is Not Necessary for Generalization. [[paper]](https://arxiv.org/abs/2109.14119) [[code]](https://github.com/JonasGeiping/fullbatchtraining)
- Jonas Geiping, Micah Goldblum, Phillip E. Pope, Michael Moeller, Tom Goldstein. *ICLR 2022*
- Key Word: Stochastic Gradient Descent; Regularization.
- Digest It is widely believed that the implicit regularization of SGD is fundamental to the impressive generalization behavior we observe in neural networks. In this work, we demonstrate that non-stochastic full-batch training can achieve comparably strong performance to SGD on CIFAR-10 using modern architectures. To this end, we show that the implicit regularization of SGD can be completely replaced with explicit regularization even when comparing against a strong and well-researched baseline.
- Pointer Value Retrieval: A new benchmark for understanding the limits of neural network generalization. [[paper]](https://arxiv.org/abs/2107.12580)
- Chiyuan Zhang, Maithra Raghu, Jon Kleinberg, Samy Bengio.
- Key Word: Out-of-Distribution Generalization.
- Digest In this paper we introduce a novel benchmark, Pointer Value Retrieval (PVR) tasks, that explore the limits of neural network generalization. We demonstrate that this task structure provides a rich testbed for understanding generalization, with our empirical study showing large variations in neural network performance based on dataset size, task complexity and model architecture.
- What can linear interpolation of neural network loss landscapes tell us? [[paper]](https://arxiv.org/abs/2106.16004)
- Tiffany Vlaar, Jonathan Frankle. *ICML 2022*
- Key Word: Linear Interpolation; Loss Landscapes.
- Digest We put inferences of this kind to the test, systematically evaluating how linear interpolation and final performance vary when altering the data, choice of initialization, and other optimizer and architecture design choices. Further, we use linear interpolation to study the role played by individual layers and substructures of the network. We find that certain layers are more sensitive to the choice of initialization, but that the shape of the linear path is not indicative of the changes in test accuracy of the model.
- Can Vision Transformers Learn without Natural Images? [[paper]](https://arxiv.org/abs/2103.13023) [[code]](https://hirokatsukataoka16.github.io/Vision-Transformers-without-Natural-Images/)
- Kodai Nakashima, Hirokatsu Kataoka, Asato Matsumoto, Kenji Iwata, Nakamasa Inoue. *AAAI 2022*
- Key Word: Formula-driven Supervised Learning; Vision Transformer.
- Digest We pre-train ViT without any image collections and annotation labor. We experimentally verify that our proposed framework partially outperforms sophisticated Self-Supervised Learning (SSL) methods like SimCLRv2 and MoCov2 without using any natural images in the pre-training phase. Moreover, although the ViT pre-trained without natural images produces some different visualizations from ImageNet pre-trained ViT, it can interpret natural image datasets to a large extent.
- The Low-Rank Simplicity Bias in Deep Networks. [[paper]](https://arxiv.org/abs/2103.10427)
- Minyoung Huh, Hossein Mobahi, Richard Zhang, Brian Cheung, Pulkit Agrawal, Phillip Isola.
- Key Word: Low-Rank Embedding; Inductive Bias.
- Digest We make a series of empirical observations that investigate and extend the hypothesis that deeper networks are inductively biased to find solutions with lower effective rank embeddings. We conjecture that this bias exists because the volume of functions that maps to low effective rank embedding increases with depth. We show empirically that our claim holds true on finite width linear and non-linear models on practical learning paradigms and show that on natural data, these are often the solutions that generalize well.
- Gradient Descent on Neural Networks Typically Occurs at the Edge of Stability. [[paper]](https://arxiv.org/abs/2103.00065) [[code]](https://github.com/locuslab/edge-of-stability)
- Jeremy M. Cohen, Simran Kaur, Yuanzhi Li, J. Zico Kolter, Ameet Talwalkar. *ICLR 2021*
- Key Word: Edge of Stability.
- Digest We empirically demonstrate that full-batch gradient descent on neural network training objectives typically operates in a regime we call the Edge of Stability. In this regime, the maximum eigenvalue of the training loss Hessian hovers just above the numerical value 2/(step size), and the training loss behaves non-monotonically over short timescales, yet consistently decreases over long timescales. Since this behavior is inconsistent with several widespread presumptions in the field of optimization, our findings raise questions as to whether these presumptions are relevant to neural network training.
- Pre-training without Natural Images. [[paper]](https://arxiv.org/abs/2101.08515) [[code]](https://github.com/hirokatsukataoka16/FractalDB-Pretrained-ResNet-PyTorch)
- Hirokatsu Kataoka, Kazushige Okayasu, Asato Matsumoto, Eisuke Yamagata, Ryosuke Yamada, Nakamasa Inoue, Akio Nakamura, Yutaka Satoh. *ACCV 2020*
- Key Word: Formula-driven Supervised Learning.
- Digest The paper proposes a novel concept, Formula-driven Supervised Learning. We automatically generate image patterns and their category labels by assigning fractals, which are based on a natural law existing in the background knowledge of the real world. Theoretically, the use of automatically generated images instead of natural images in the pre-training phase allows us to generate an infinite scale dataset of labeled images. Although the models pre-trained with the proposed Fractal DataBase (FractalDB), a database without natural images, does not necessarily outperform models pre-trained with human annotated datasets at all settings, we are able to partially surpass the accuracy of ImageNet/Places pre-trained models.
### Empirical Study: 2020
- When Do Curricula Work? [[paper]](https://arxiv.org/abs/2012.03107) [[code]](https://github.com/google-research/understanding-curricula)
- Xiaoxia Wu, Ethan Dyer, Behnam Neyshabur. *ICLR 2021*
- Key Word: Curriculum Learning.
- Digest We set out to investigate the relative benefits of ordered learning. We first investigate the implicit curricula resulting from architectural and optimization bias and find that samples are learned in a highly consistent order. Next, to quantify the benefit of explicit curricula, we conduct extensive experiments over thousands of orderings spanning three kinds of learning: curriculum, anti-curriculum, and random-curriculum -- in which the size of the training dataset is dynamically increased over time, but the examples are randomly ordered.
- In Search of Robust Measures of Generalization. [[paper]](https://arxiv.org/abs/2010.11924) [[code]](https://github.com/nitarshan/robust-generalization-measures)
- Gintare Karolina Dziugaite, Alexandre Drouin, Brady Neal, Nitarshan Rajkumar, Ethan Caballero, Linbo Wang, Ioannis Mitliagkas, Daniel M. Roy. *NeurIPS 2020*
- Key Word: Generalization Measures.
- Digest One of the principal scientific challenges in deep learning is explaining generalization, i.e., why the particular way the community now trains networks to achieve small training error also leads to small error on held-out data from the same population. It is widely appreciated that some worst-case theories -- such as those based on the VC dimension of the class of predictors induced by modern neural network architectures -- are unable to explain empirical performance. A large volume of work aims to close this gap, primarily by developing bounds on generalization error, optimization error, and excess risk. When evaluated empirically, however, most of these bounds are numerically vacuous. Focusing on generalization bounds, this work addresses the question of how to evaluate such bounds empirically.
- The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers. [[paper]](https://arxiv.org/abs/2010.08127) [[code]](https://github.com/preetum/deep-bootstrap-code)
- Preetum Nakkiran, Behnam Neyshabur, Hanie Sedghi. *ICLR 2021*
- Key Word: Online Learning; Finite-Sample Deviations.
- Digest We propose a new framework for reasoning about generalization in deep learning. The core idea is to couple the Real World, where optimizers take stochastic gradient steps on the empirical loss, to an Ideal World, where optimizers take steps on the population loss. This leads to an alternate decomposition of test error into: (1) the Ideal World test error plus (2) the gap between the two worlds. If the gap (2) is universally small, this reduces the problem of generalization in offline learning to the problem of optimization in online learning.
- Characterising Bias in Compressed Models. [[paper]](https://arxiv.org/abs/2010.03058)
- Sara Hooker, Nyalleng Moorosi, Gregory Clark, Samy Bengio, Emily Denton.
- Key Word: Pruning; Fairness.
- Digest The popularity and widespread use of pruning and quantization is driven by the severe resource constraints of deploying deep neural networks to environments with strict latency, memory and energy requirements. These techniques achieve high levels of compression with negligible impact on top-line metrics (top-1 and top-5 accuracy). However, overall accuracy hides disproportionately high errors on a small subset of examples; we call this subset Compression Identified Exemplars (CIE).
- Dataset Cartography: Mapping and Diagnosing Datasets with Training Dynamics. [[paper]](https://arxiv.org/abs/2009.10795) [[code]](https://github.com/allenai/cartography)
- Swabha Swayamdipta, Roy Schwartz, Nicholas Lourie, Yizhong Wang, Hannaneh Hajishirzi, Noah A. Smith, Yejin Choi. *EMNLP 2020*
- Key Word: Training Dynamics; Data Map; Curriculum Learning.
- Digest Large datasets have become commonplace in NLP research. However, the increased emphasis on data quantity has made it challenging to assess the quality of data. We introduce Data Maps---a model-based tool to characterize and diagnose datasets. We leverage a largely ignored source of information: the behavior of the model on individual instances during training (training dynamics) for building data maps.
- What is being transferred in transfer learning? [[paper]](https://arxiv.org/abs/2008.11687) [[code]](https://github.com/google-research/understanding-transfer-learning)
- Behnam Neyshabur, Hanie Sedghi, Chiyuan Zhang. *NeurIPS 2020*
- Key Word: Transfer Learning.
- Digest We provide new tools and analyses to address these fundamental questions. Through a series of analyses on transferring to block-shuffled images, we separate the effect of feature reuse from learning low-level statistics of data and show that some benefit of transfer learning comes from the latter. We present that when training from pre-trained weights, the model stays in the same basin in the loss landscape and different instances of such model are similar in feature space and close in parameter space.
- Deep Isometric Learning for Visual Recognition. [[paper]](https://arxiv.org/abs/2006.16992) [[code]](https://github.com/HaozhiQi/ISONet)
- Haozhi Qi, Chong You, Xiaolong Wang, Yi Ma, Jitendra Malik. *ICML 2020*
- Key Word: Isometric Networks.
- Digest This paper shows that deep vanilla ConvNets without normalization nor skip connections can also be trained to achieve surprisingly good performance on standard image recognition benchmarks. This is achieved by enforcing the convolution kernels to be near isometric during initialization and training, as well as by using a variant of ReLU that is shifted towards being isometric.
- On the Generalization Benefit of Noise in Stochastic Gradient Descent. [[paper]](https://arxiv.org/abs/2006.15081)
- Samuel L. Smith, Erich Elsen, Soham De. *ICML 2020*
- Key Word: Stochastic Gradient Descent.
- Digest In this paper, we perform carefully designed experiments and rigorous hyperparameter sweeps on a range of popular models, which verify that small or moderately large batch sizes can substantially outperform very large batches on the test set. This occurs even when both models are trained for the same number of iterations and large batches achieve smaller training losses.
- Do CNNs Encode Data Augmentations? [[paper]](https://arxiv.org/abs/2003.08773)
- Eddie Yan, Yanping Huang.
- Key Word: Data Augmentations.
- Digest Surprisingly, neural network features not only predict data augmentation transformations, but they predict many transformations with high accuracy. After validating that neural networks encode features corresponding to augmentation transformations, we show that these features are primarily encoded in the early layers of modern CNNs.
- Do We Need Zero Training Loss After Achieving Zero Training Error? [[paper]](https://arxiv.org/abs/2002.08709) [[code]](https://github.com/takashiishida/flooding)
- Takashi Ishida, Ikko Yamane, Tomoya Sakai, Gang Niu, Masashi Sugiyama. *ICML 2020*
- Key Word: Regularization.
- Digest Our approach makes the loss float around the flooding level by doing mini-batched gradient descent as usual but gradient ascent if the training loss is below the flooding level. This can be implemented with one line of code, and is compatible with any stochastic optimizer and other regularizers. We experimentally show that flooding improves performance and as a byproduct, induces a double descent curve of the test loss.
- Understanding Why Neural Networks Generalize Well Through GSNR of Parameters. [[paper]](https://arxiv.org/abs/2001.07384)
- Jinlong Liu, Guoqing Jiang, Yunzhi Bai, Ting Chen, Huayan Wang. *ICLR 2020*
- Key Word: Generalization Indicators.
- Digest In this paper, we provide a novel perspective on these issues using the gradient signal to noise ratio (GSNR) of parameters during training process of DNNs. The GSNR of a parameter is defined as the ratio between its gradient's squared mean and variance, over the data distribution.
### Empirical Study: 2019
- Angular Visual Hardness. [[paper]](https://arxiv.org/abs/1912.02279)
- Beidi Chen, Weiyang Liu, Zhiding Yu, Jan Kautz, Anshumali Shrivastava, Animesh Garg, Anima Anandkumar. *ICML 2020*
- Key Word: Calibration; Example Hardness Measures.
- Digest We propose a novel measure for CNN models known as Angular Visual Hardness. Our comprehensive empirical studies show that AVH can serve as an indicator of generalization abilities of neural networks, and improving SOTA accuracy entails improving accuracy on hard example
- Fantastic Generalization Measures and Where to Find Them. [[paper]](https://arxiv.org/abs/1912.02178) [[code]](https://github.com/avakanski/Evaluation-of-Complexity-Measures-for-Deep-Learning-Generalization-in-Medical-Image-Analysis)
- Yiding Jiang, Behnam Neyshabur, Hossein Mobahi, Dilip Krishnan, Samy Bengio. *ICLR 2020*
- Key Word: Complexity Measures; Spurious Correlations.
- Digest We present the first large scale study of generalization in deep networks. We investigate more then 40 complexity measures taken from both theoretical bounds and empirical studies. We train over 10,000 convolutional networks by systematically varying commonly used hyperparameters. Hoping to uncover potentially causal relationships between each measure and generalization, we analyze carefully controlled experiments and show surprising failures of some measures as well as promising measures for further research.
- Truth or Backpropaganda? An Empirical Investigation of Deep Learning Theory. [[paper]](https://arxiv.org/abs/1910.00359) [[code]](https://github.com/goldblum/TruthOrBackpropaganda)
- Micah Goldblum, Jonas Geiping, Avi Schwarzschild, Michael Moeller, Tom Goldstein. *ICLR 2020*
- Key Word: Local Minima.
- Digest The authors take a closer look at widely held beliefs about neural networks. Using a mix of analysis and experiment, they shed some light on the ways these assumptions break down.
- Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML. [[paper]](https://arxiv.org/abs/1909.09157) [[code]](https://github.com/fmu2/PyTorch-MAML)
- Aniruddh Raghu, Maithra Raghu, Samy Bengio, Oriol Vinyals. *ICLR 2020*
- Key Word: Meta Learning.
- Digest Despite MAML's popularity, a fundamental open question remains -- is the effectiveness of MAML due to the meta-initialization being primed for rapid learning (large, efficient changes in the representations) or due to feature reuse, with the meta initialization already containing high quality features? We investigate this question, via ablation studies and analysis of the latent representations, finding that feature reuse is the dominant factor.
- Finding the Needle in the Haystack with Convolutions: on the benefits of architectural bias. [[paper]](https://arxiv.org/abs/1906.06766) [[code]](https://github.com/sdascoli/anarchitectural-search)
- Stéphane d'Ascoli, Levent Sagun, Joan Bruna, Giulio Biroli. *NeurIPS 2019*
- Key Word: Architectural Bias.
- Digest In particular, Convolutional Neural Networks (CNNs) are known to perform much better than Fully-Connected Networks (FCNs) on spatially structured data: the architectural structure of CNNs benefits from prior knowledge on the features of the data, for instance their translation invariance. The aim of this work is to understand this fact through the lens of dynamics in the loss landscape.
- Adversarial Training Can Hurt Generalization. [[paper]](https://arxiv.org/abs/1906.06032)
- Aditi Raghunathan, Sang Michael Xie, Fanny Yang, John C. Duchi, Percy Liang.
- Key Word: Adversarial Examples.
- Digest While adversarial training can improve robust accuracy (against an adversary), it sometimes hurts standard accuracy (when there is no adversary). Previous work has studied this tradeoff between standard and robust accuracy, but only in the setting where no predictor performs well on both objectives in the infinite data limit. In this paper, we show that even when the optimal predictor with infinite data performs well on both objectives, a tradeoff can still manifest itself with finite data.
- Bad Global Minima Exist and SGD Can Reach Them. [[paper]](https://arxiv.org/abs/1906.02613) [[code]](https://github.com/chao1224/BadGlobalMinima)
- Shengchao Liu, Dimitris Papailiopoulos, Dimitris Achlioptas. *NeurIPS 2020*
- Key Word: Stochastic Gradient Descent.
- Digest Several works have aimed to explain why overparameterized neural networks generalize well when trained by Stochastic Gradient Descent (SGD). The consensus explanation that has emerged credits the randomized nature of SGD for the bias of the training process towards low-complexity models and, thus, for implicit regularization. We take a careful look at this explanation in the context of image classification with common deep neural network architectures. We find that if we do not regularize explicitly, then SGD can be easily made to converge to poorly-generalizing, high-complexity models: all it takes is to first train on a random labeling on the data, before switching to properly training with the correct labels.
- Deep ReLU Networks Have Surprisingly Few Activation Patterns. [[paper]](https://arxiv.org/abs/1906.00904)
- Boris Hanin, David Rolnick. *NeurIPS 2019*
- Digest In this paper, we show that the average number of activation patterns for ReLU networks at initialization is bounded by the total number of neurons raised to the input dimension. We show empirically that this bound, which is independent of the depth, is tight both at initialization and during training, even on memorization tasks that should maximize the number of activation patterns.
- Sensitivity of Deep Convolutional Networks to Gabor Noise. [[paper]](https://arxiv.org/abs/1906.03455) [[code]](https://github.com/kenny-co/procedural-advml)
- Kenneth T. Co, Luis Muñoz-González, Emil C. Lupu.
- Key Word: Robustness.
- Digest Deep Convolutional Networks (DCNs) have been shown to be sensitive to Universal Adversarial Perturbations (UAPs): input-agnostic perturbations that fool a model on large portions of a dataset. These UAPs exhibit interesting visual patterns, but this phenomena is, as yet, poorly understood. Our work shows that visually similar procedural noise patterns also act as UAPs. In particular, we demonstrate that different DCN architectures are sensitive to Gabor noise patterns. This behaviour, its causes, and implications deserve further in-depth study.
- Rethinking the Usage of Batch Normalization and Dropout in the Training of Deep Neural Networks. [[paper]](https://arxiv.org/abs/1905.05928)
- Guangyong Chen, Pengfei Chen, Yujun Shi, Chang-Yu Hsieh, Benben Liao, Shengyu Zhang.
- Key Word: Batch Normalization; Dropout.
- Digest Our work is based on an excellent idea that whitening the inputs of neural networks can achieve a fast convergence speed. Given the well-known fact that independent components must be whitened, we introduce a novel Independent-Component (IC) layer before each weight layer, whose inputs would be made more independent.
- A critical analysis of self-supervision, or what we can learn from a single image. [[paper]](https://arxiv.org/abs/1904.13132) [[code]](https://github.com/yukimasano/linear-probes)
- Yuki M. Asano, Christian Rupprecht, Andrea Vedaldi. *ICLR 2020*
- Key Word: Self-Supervision.
- Digest We show that three different and representative methods, BiGAN, RotNet and DeepCluster, can learn the first few layers of a convolutional network from a single image as well as using millions of images and manual labels, provided that strong data augmentation is used. However, for deeper layers the gap with manual supervision cannot be closed even if millions of unlabelled images are used for training.
- Approximating CNNs with Bag-of-local-Features models works surprisingly well on ImageNet. [[paper]](https://arxiv.org/abs/1904.00760) [[code]](https://github.com/wielandbrendel/bag-of-local-features-models)
- Wieland Brendel, Matthias Bethge. *ICLR 2019*
- Key Word: Bag-of-Features.
- Digest Our model, a simple variant of the ResNet-50 architecture called BagNet, classifies an image based on the occurrences of small local image features without taking into account their spatial ordering. This strategy is closely related to the bag-of-feature (BoF) models popular before the onset of deep learning and reaches a surprisingly high accuracy on ImageNet.
- Transfusion: Understanding Transfer Learning for Medical Imaging. [[paper]](https://arxiv.org/abs/1902.07208) [[code]](https://github.com/PasqualeZingo/TransfusionReproducibilityChallenge)
- Maithra Raghu, Chiyuan Zhang, Jon Kleinberg, Samy Bengio. *NeurIPS 2019*
- Key Word: Transfer Learning; Medical Imaging.
- Digest we explore properties of transfer learning for medical imaging. A performance evaluation on two large scale medical imaging tasks shows that surprisingly, transfer offers little benefit to performance, and simple, lightweight models can perform comparably to ImageNet architectures.
- Identity Crisis: Memorization and Generalization under Extreme Overparameterization. [[paper]](https://arxiv.org/abs/1902.04698)
- Chiyuan Zhang, Samy Bengio, Moritz Hardt, Michael C. Mozer, Yoram Singer. *ICLR 2020*
- Key Word: Memorization.
- Digest We study the interplay between memorization and generalization of overparameterized networks in the extreme case of a single training example and an identity-mapping task.
- Are All Layers Created Equal? [[paper]](https://arxiv.org/abs/1902.01996)
- Chiyuan Zhang, Samy Bengio, Yoram Singer. *JMLR*
- Key Word: Robustness.
- Digest We show that the layers can be categorized as either "ambient" or "critical". Resetting the ambient layers to their initial values has no negative consequence, and in many cases they barely change throughout training. On the contrary, resetting the critical layers completely destroys the predictor and the performance drops to chance.
### Empirical Study: 2018
- Why ReLU networks yield high-confidence predictions far away from the training data and how to mitigate the problem. [[paper]](https://arxiv.org/abs/1812.05720) [[code]](https://github.com/max-andr/relu_networks_overconfident)
- Matthias Hein, Maksym Andriushchenko, Julian Bitterwolf. *CVPR 2019*
- Key Word: ReLU.
- Digest Classifiers used in the wild, in particular for safety-critical systems, should not only have good generalization properties but also should know when they don't know, in particular make low confidence predictions far away from the training data. We show that ReLU type neural networks which yield a piecewise linear classifier function fail in this regard as they produce almost always high confidence predictions far away from the training data.
- An Empirical Study of Example Forgetting during Deep Neural Network Learning. [[paper]](https://arxiv.org/abs/1812.05159) [[code]](https://github.com/mtoneva/example_forgetting)
- Mariya Toneva, Alessandro Sordoni, Remi Tachet des Combes, Adam Trischler, Yoshua Bengio, Geoffrey J. Gordon. *ICLR 2019*
- Key Word: Curriculum Learning; Sample Weighting; Example Forgetting.
- Digest We define a 'forgetting event' to have occurred when an individual training example transitions from being classified correctly to incorrectly over the course of learning. Across several benchmark data sets, we find that: (i) certain examples are forgotten with high frequency, and some not at all; (ii) a data set's (un)forgettable examples generalize across neural architectures; and (iii) based on forgetting dynamics, a significant fraction of examples can be omitted from the training data set while still maintaining state-of-the-art generalization performance.
- On Implicit Filter Level Sparsity in Convolutional Neural Networks. [[paper]](https://arxiv.org/abs/1811.12495)
- Dushyant Mehta, Kwang In Kim, Christian Theobalt. *CVPR 2019*
- Key Word: Regularization; Sparsification.
- Digest We investigate filter level sparsity that emerges in convolutional neural networks (CNNs) which employ Batch Normalization and ReLU activation, and are trained with adaptive gradient descent techniques and L2 regularization or weight decay. We conduct an extensive experimental study casting our initial findings into hypotheses and conclusions about the mechanisms underlying the emergent filter level sparsity. This study allows new insight into the performance gap obeserved between adapative and non-adaptive gradient descent methods in practice.
- Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations. [[paper]](https://arxiv.org/abs/1811.12359) [[code]](https://github.com/google-research/disentanglement_lib)
- Francesco Locatello, Stefan Bauer, Mario Lucic, Gunnar Rätsch, Sylvain Gelly, Bernhard Schölkopf, Olivier Bachem. *ICML 2019*
- Key Word: Disentanglement.
- Digest Our results suggest that future work on disentanglement learning should be explicit about the role of inductive biases and (implicit) supervision, investigate concrete benefits of enforcing disentanglement of the learned representations, and consider a reproducible experimental setup covering several data sets.
- Insights on representational similarity in neural networks with canonical correlation. [[paper]](https://arxiv.org/abs/1806.05759) [[code]](https://github.com/google/svcca)
- Ari S. Morcos, Maithra Raghu, Samy Bengio. *NeurIPS 2018*
- Key Word: Representational Similarity.
- Digest Comparing representations in neural networks is fundamentally difficult as the structure of representations varies greatly, even across groups of networks trained on identical tasks, and over the course of training. Here, we develop projection weighted CCA (Canonical Correlation Analysis) as a tool for understanding neural networks, building off of SVCCA.
- Layer rotation: a surprisingly powerful indicator of generalization in deep networks? [[paper]](https://arxiv.org/abs/1806.01603) [[code]](https://github.com/ispgroupucl/layer-rotation-paper-experiments)
- Simon Carbonnelle, Christophe De Vleeschouwer.
- Key Word: Weight Evolution.
- Digest Our work presents extensive empirical evidence that layer rotation, i.e. the evolution across training of the cosine distance between each layer's weight vector and its initialization, constitutes an impressively consistent indicator of generalization performance. In particular, larger cosine distances between final and initial weights of each layer consistently translate into better generalization performance of the final model.
- Sensitivity and Generalization in Neural Networks: an Empirical Study. [[paper]](https://arxiv.org/abs/1802.08760)
- Roman Novak, Yasaman Bahri, Daniel A. Abolafia, Jeffrey Pennington, Jascha Sohl-Dickstein. *ICLR 2018*
- Key Word: Sensitivity.
- Digest In this work, we investigate this tension between complexity and generalization through an extensive empirical exploration of two natural metrics of complexity related to sensitivity to input perturbations. We find that trained neural networks are more robust to input perturbations in the vicinity of the training data manifold, as measured by the norm of the input-output Jacobian of the network, and that it correlates well with generalization.
### Empirical Study: 2017
- Deep Image Prior. [[paper]](https://arxiv.org/abs/1711.10925) [[code]](https://dmitryulyanov.github.io/deep_image_prior)
- Dmitry Ulyanov, Andrea Vedaldi, Victor Lempitsky.
- Key Word: Low-Level Vision.
- Digest In this paper, we show that, on the contrary, the structure of a generator network is sufficient to capture a great deal of low-level image statistics prior to any learning. In order to do so, we show that a randomly-initialized neural network can be used as a handcrafted prior with excellent results in standard inverse problems such as denoising, super-resolution, and inpainting.
- Critical Learning Periods in Deep Neural Networks. [[paper]](https://arxiv.org/abs/1711.08856)
- Alessandro Achille, Matteo Rovere, Stefano Soatto. *ICLR 2019*
- Key Word: Memorization.
- Digest Our findings indicate that the early transient is critical in determining the final solution of the optimization associated with training an artificial neural network. In particular, the effects of sensory deficits during a critical period cannot be overcome, no matter how much additional training is performed.
- A Closer Look at Memorization in Deep Networks. [[paper]](https://arxiv.org/abs/1706.05394)
- Devansh Arpit, Stanisław Jastrzębski, Nicolas Ballas, David Krueger, Emmanuel Bengio, Maxinder S. Kanwal, Tegan Maharaj, Asja Fischer, Aaron Courville, Yoshua Bengio, Simon Lacoste-Julien. *ICML 2017*
- Key Word: Memorization.
- Digest In our experiments, we expose qualitative differences in gradient-based optimization of deep neural networks (DNNs) on noise vs. real data. We also demonstrate that for appropriately tuned explicit regularization (e.g., dropout) we can degrade DNN training performance on noise datasets without compromising generalization on real data.
### Empirical Study: 2016
- Understanding deep learning requires rethinking generalization. [[paper]](https://arxiv.org/abs/1611.03530)
- Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, Oriol Vinyals. *ICLR 2017*
- Key Word: Memorization.
- Digest Through extensive systematic experiments, we show how these traditional approaches fail to explain why large neural networks generalize well in practice. Specifically, our experiments establish that state-of-the-art convolutional networks for image classification trained with stochastic gradient methods easily fit a random labeling of the training data.
## Neural Collapse

### Neural Collapse: 2025
- Neural Collapse Beyond the Unconstrainted Features Model: Landscape, Dynamics, and Generalization in the Mean-Field Regime. [[paper]](https://arxiv.org/abs/2501.19104)
- Diyuan Wu, Marco Mondelli.
- Key Word: Neural Collapse; Mean-Field Analysis.
- Digest This paper studies Neural Collapse (NC1)—the vanishing of within-class variability in well-trained neural networks—from a data-specific perspective. Analyzing a three-layer network with mean-field dynamics, the authors establish a key link between NC1 and the loss landscape, proving that points with small loss and gradient norm approximately satisfy NC1. They further show that gradient flow on MSE loss leads to NC1 solutions and that for well-separated data, NC1 coincides with vanishing test error. The results highlight how NC1 naturally emerges during training due to loss landscape properties.
### Neural Collapse: 2024
- Formation of Representations in Neural Networks. [[paper]](https://arxiv.org/abs/2410.03006)
- Liu Ziyin, Isaac Chuang, Tomer Galanti, Tomaso Poggio.
- Key Word: Canonical Representation Hypothesis; Neural Representation.
- Digest This paper proposes the Canonical Representation Hypothesis (CRH), which posits that during neural network training, a set of six alignment relations universally governs the formation of representations in hidden layers. Specifically, it suggests that the latent representations (R), weights (W), and neuron gradients (G) become mutually aligned, leading to compact representations that are invariant to task-irrelevant transformations. The paper also introduces the Polynomial Alignment Hypothesis (PAH), which arises when CRH is broken, resulting in power-law relations between R, W, and G. The authors suggest that balancing gradient noise and regularization is key to the emergence of these canonical representations and propose that these hypotheses could unify major deep learning phenomena like neural collapse and the neural feature ansatz.
- Neural Collapse Meets Differential Privacy: Curious Behaviors of NoisyGD with Near-perfect Representation Learning. [[paper]](https://arxiv.org/abs/2405.08920)
- Chendi Wang, Yuqing Zhu, Weijie J. Su, Yu-Xiang Wang.
- key Word: Neural Collapse; Differential Privacy.
- Digest The study by De et al. (2022) explores the impact of large-scale representation learning on differentially private (DP) learning, focusing on the phenomenon of Neural Collapse (NC) in deep learning and transfer learning. The research establishes an error bound within the NC framework, evaluates feature quality, reveals the lesser robustness of DP fine-tuning, and suggests strategies to enhance its robustness, with empirical evidence supporting these findings.
- Average gradient outer product as a mechanism for deep neural collapse. [[paper]](https://arxiv.org/abs/2402.13728)
- Daniel Beaglehole, Peter Súkeník, Marco Mondelli, Mikhail Belkin.
- Key Word: Neural Collapse; Average Gradient Outer Product.
- Digest This paper investigates the phenomenon of Deep Neural Collapse (DNC), where the final layers of Deep Neural Networks (DNNs) exhibit a highly structured representation of data. The study presents significant evidence that DNC primarily occurs through the process of deep feature learning, facilitated by the average gradient outer product (AGOP). This approach marks a departure from previous explanations that relied on feature-agnostic models. The authors highlight the role of the right singular vectors and values of the network weights in reducing within-class variability, a key aspect of DNC. They establish a link between this singular structure and the AGOP, further demonstrating experimentally and theoretically that AGOP can induce DNC even in randomly initialized neural networks. The paper also discusses Deep Recursive Feature Machines, a conceptual method representing AGOP feature learning in convolutional neural networks, and shows its capability to exhibit DNC.
- Pushing Boundaries: Mixup's Influence on Neural Collapse. [[paper]](https://arxiv.org/abs/2402.06171)
- Quinn Fisher, Haoming Meng, Vardan Papyan.
- Key Word: Mixup; Neural Collapse.
- Digest The abstract investigates "Mixup," a technique enhancing deep neural network robustness by blending training data and labels, focusing on its success through geometric configurations of network activations. It finds that mixup leads to a unique alignment of last-layer activations that challenges prior expectations, with mixed examples of the same class aligning with the classifier and different classes marking distinct boundaries. This unexpected behavior suggests mixup affects deeper network layers in a novel way, diverging from simple convex combinations of class features. The study connects these findings to improved model calibration and supports them with a theoretical analysis, highlighting the role of a specific geometric pattern (simplex equiangular tight frame) in optimizing last-layer features for better performance.
### Neural Collapse: 2023
- Are Neurons Actually Collapsed? On the Fine-Grained Structure in Neural Representations. [[paper]](https://arxiv.org/abs/2306.17105)
- Yongyi Yang, Jacob Steinhardt, Wei Hu. *ICML 2023*
- Key Word: Neural Collapse.
- Digest The paper challenges the notion of "Neural Collapse" in well-trained neural networks, arguing that while the last-layer representations may appear to collapse, there is still fine-grained structure present in the representations that captures the intrinsic structure of the input distribution.
- Neural (Tangent Kernel) Collapse. [[paper]](https://arxiv.org/abs/2305.16427)
- Mariia Seleznova, Dana Weitzner, Raja Giryes, Gitta Kutyniok, Hung-Hsu Chou.
- Key Word: Neural Collapse; Neural Tangent Kernel.
- Digest This paper investigates how the Neural Tangent Kernel (NTK), which tracks how deep neural networks (DNNs) change during training, and the Neural Collapse (NC) phenomenon, which refers to the symmetry and structure in the last-layer features of trained classification DNNs, are related. They assume that the empirical NTK has a block structure that matches the class labels, meaning that samples of the same class are more correlated than samples of different classes. They show how this assumption leads to the dynamics of DNNs trained with mean squared (MSE) loss and the emergence of NC in DNNs with block-structured NTK. They support their theory with large-scale experiments on three DNN architectures and three datasets.
- Neural Collapse Inspired Feature-Classifier Alignment for Few-Shot Class Incremental Learning. [[paper]](https://arxiv.org/abs/2302.03004) [[code]](https://github.com/NeuralCollapseApplications/FSCIL)
- Yibo Yang, Haobo Yuan, Xiangtai Li, Zhouchen Lin, Philip Torr, Dacheng Tao. *ICLR 2023*
- Key Word: Few-Shot Class Incremental Learning; Neural Collapse.
- Digest We deal with this misalignment dilemma in FSCIL inspired by the recently discovered phenomenon named neural collapse, which reveals that the last-layer features of the same class will collapse into a vertex, and the vertices of all classes are aligned with the classifier prototypes, which are formed as a simplex equiangular tight frame (ETF). It corresponds to an optimal geometric structure for classification due to the maximized Fisher Discriminant Ratio.
- Neural Collapse in Deep Linear Network: From Balanced to Imbalanced Data. [[paper]](https://arxiv.org/abs/2301.00437)
- Hien Dang, Tan Nguyen, Tho Tran, Hung Tran, Nhat Ho.
- Key Word: Neural Collapse; Imbalanced Learning.
- Digest We take a step further and prove the Neural Collapse occurrence for deep linear network for the popular mean squared error (MSE) and cross entropy (CE) loss. Furthermore, we extend our research to imbalanced data for MSE loss and present the first geometric analysis for Neural Collapse under this setting.
### Neural Collapse: 2022
- Principled and Efficient Transfer Learning of Deep Models via Neural Collapse. [[paper]](https://arxiv.org/abs/2212.12206)
- Xiao Li, Sheng Liu, Jinxin Zhou, Xinyu Lu, Carlos Fernandez-Granda, Zhihui Zhu, Qing Qu.
- Key Word: Neural Collapse; Transfer Learning.
- Digest This work delves into the mystery of transfer learning through an intriguing phenomenon termed neural collapse (NC), where the last-layer features and classifiers of learned deep networks satisfy: (i) the within-class variability of the features collapses to zero, and (ii) the between-class feature means are maximally and equally separated. Through the lens of NC, our findings for transfer learning are the following: (i) when pre-training models, preventing intra-class variability collapse (to a certain extent) better preserves the intrinsic structures of the input data, so that it leads to better model transferability; (ii) when fine-tuning models on downstream tasks, obtaining features with more NC on downstream data results in better test accuracy on the given task.
- Perturbation Analysis of Neural Collapse. [[paper]](https://arxiv.org/abs/2210.16658)
- Tom Tirer, Haoxiang Huang, Jonathan Niles-Weed.
- Key Word: Neural Collapse.
- Digest We propose a richer model that can capture this phenomenon by forcing the features to stay in the vicinity of a predefined features matrix (e.g., intermediate features). We explore the model in the small vicinity case via perturbation analysis and establish results that cannot be obtained by the previously studied models.
- Imbalance Trouble: Revisiting Neural-Collapse Geometry. [[paper]](https://arxiv.org/abs/2208.05512)
- Christos Thrampoulidis, Ganesh R. Kini, Vala Vakilian, Tina Behnia.
- Key Word: Neural Collapse; Class Imbalance.
- Digest Neural Collapse refers to the remarkable structural properties characterizing the geometry of class embeddings and classifier weights, found by deep nets when trained beyond zero training error. However, this characterization only holds for balanced data. Here we thus ask whether it can be made invariant to class imbalances. Towards this end, we adopt the unconstrained-features model (UFM), a recent theoretical model for studying neural collapse, and introduce Simplex-Encoded-Labels Interpolation (SELI) as an invariant characterization of the neural collapse phenomenon.
- Neural Collapse: A Review on Modelling Principles and Generalization. [[paper]](https://arxiv.org/abs/2206.04041)
- Vignesh Kothapalli, Ebrahim Rasromani, Vasudev Awatramani.
- Key Word: Neural Collapse.
- Digest We analyse the principles which aid in modelling such a phenomena from the ground up and show how they can build a common understanding of the recently proposed models that try to explain NC. We hope that our analysis presents a multifaceted perspective on modelling NC and aids in forming connections with the generalization capabilities of neural networks. Finally, we conclude by discussing the avenues for further research and propose potential research problems.
- Do We Really Need a Learnable Classifier at the End of Deep Neural Network? [[paper]](https://arxiv.org/abs/2203.09081)
- Yibo Yang, Liang Xie, Shixiang Chen, Xiangtai Li, Zhouchen Lin, Dacheng Tao.
- Key Word: Neural Collapse.
- Digest We study the potential of training a network with the last-layer linear classifier randomly initialized as a simplex ETF and fixed during training. This practice enjoys theoretical merits under the layer-peeled analytical framework. We further develop a simple loss function specifically for the ETF classifier. Its advantage gets verified by both theoretical and experimental results.
- Limitations of Neural Collapse for Understanding Generalization in Deep Learning. [[paper]](https://arxiv.org/abs/2202.08384)
- Like Hui, Mikhail Belkin, Preetum Nakkiran.
- Key Word: Neural Collapse.
- Digest We point out that Neural Collapse is primarily an optimization phenomenon, not a generalization one, by investigating the train collapse and test collapse on various dataset and architecture combinations. We propose more precise definitions — "strong" and "weak" Neural Collapse for both the train set and the test set — and discuss their theoretical feasibility.
### Neural Collapse: 2021
- On the Role of Neural Collapse in Transfer Learning. [[paper]](https://arxiv.org/abs/2112.15121)
- Tomer Galanti, András György, Marcus Hutter. *ICLR 2022*
- Key Word: Neural Collapse; Transfer Learning.
- Digest We provide an explanation for this behavior based on the recently observed phenomenon that the features learned by overparameterized classification networks show an interesting clustering property, called neural collapse.
- An Unconstrained Layer-Peeled Perspective on Neural Collapse. [[paper]](https://arxiv.org/abs/2110.02796)
- Wenlong Ji, Yiping Lu, Yiliang Zhang, Zhun Deng, Weijie J. Su. *ICLR 2022*
- Key Word: Neural Collapse; Uncostrained Model; Implicit Regularization.
- Digest We introduce a surrogate model called the unconstrained layer-peeled model (ULPM). We prove that gradient flow on this model converges to critical points of a minimum-norm separation problem exhibiting neural collapse in its global minimizer. Moreover, we show that the ULPM with the cross-entropy loss has a benign global landscape for its loss function, which allows us to prove that all the critical points are strict saddle points except the global minimizers that exhibit the neural collapse phenomenon.
- Neural Collapse Under MSE Loss: Proximity to and Dynamics on the Central Path. [[paper]](https://arxiv.org/abs/2106.02073)
- X.Y. Han, Vardan Papyan, David L. Donoho. *ICLR 2022*
- Key Word: Neural Collapse; Gradient Flow.
- Digest The analytically-tractable MSE loss offers more mathematical opportunities than the hard-to-analyze CE loss, inspiring us to leverage MSE loss towards the theoretical investigation of NC. We develop three main contributions: (I) We show a new decomposition of the MSE loss into (A) terms directly interpretable through the lens of NC and which assume the last-layer classifier is exactly the least-squares classifier; and (B) a term capturing the deviation from this least-squares classifier. (II) We exhibit experiments on canonical datasets and networks demonstrating that term-(B) is negligible during training. This motivates us to introduce a new theoretical construct: the central path, where the linear classifier stays MSE-optimal for feature activations throughout the dynamics. (III) By studying renormalized gradient flow along the central path, we derive exact dynamics that predict NC.
- A Geometric Analysis of Neural Collapse with Unconstrained Features. [[paper]](https://arxiv.org/abs/2105.02375) [[code]](https://github.com/tding1/Neural-Collapse)
- Zhihui Zhu, Tianyu Ding, Jinxin Zhou, Xiao Li, Chong You, Jeremias Sulam, Qing Qu. *NeurIPS 2021*
- Key Word: Neural Collapse, Nonconvex Optimization.
- Digest We provide the first global optimization landscape analysis of Neural Collapse -- an intriguing empirical phenomenon that arises in the last-layer classifiers and features of neural networks during the terminal phase of training. As recently reported by Papyan et al., this phenomenon implies that (i) the class means and the last-layer classifiers all collapse to the vertices of a Simplex Equiangular Tight Frame (ETF) up to scaling, and (ii) cross-example within-class variability of last-layer activations collapses to zero. We study the problem based on a simplified unconstrained feature model, which isolates the topmost layers from the classifier of the neural network.
- Exploring Deep Neural Networks via Layer-Peeled Model: Minority Collapse in Imbalanced Training. [[paper]](https://arxiv.org/abs/2101.12699) [[code]](https://github.com/HornHehhf/LPM)
- Cong Fang, Hangfeng He, Qi Long, Weijie J. Su. *PNAS*
- Key Word: Neural Collapse; Imbalanced Training.
- Digest In this paper, we introduce the Layer-Peeled Model, a nonconvex yet analytically tractable optimization program, in a quest to better understand deep neural networks that are trained for a sufficiently long time. As the name suggests, this new model is derived by isolating the topmost layer from the remainder of the neural network, followed by imposing certain constraints separately on the two parts of the network. When moving to the imbalanced case, our analysis of the Layer-Peeled Model reveals a hitherto unknown phenomenon that we term Minority Collapse, which fundamentally limits the performance of deep learning models on the minority classes.
### Neural Collapse: 2020
- Prevalence of Neural Collapse during the terminal phase of deep learning training. [[paper]](https://arxiv.org/abs/2008.08186) [[code]](https://github.com/neuralcollapse/neuralcollapse)
- Vardan Papyan, X.Y. Han, David L. Donoho. *PNAS*
- Key Word: Neural Collapse.
- Digest This paper studied the terminal phase of training (TPT) of today’s canonical deepnet training protocol. It documented that during TPT a process called Neural Collapse takes place, involving four fundamental and interconnected phenomena: (NC1)-(NC4).
## Deep Double Descent
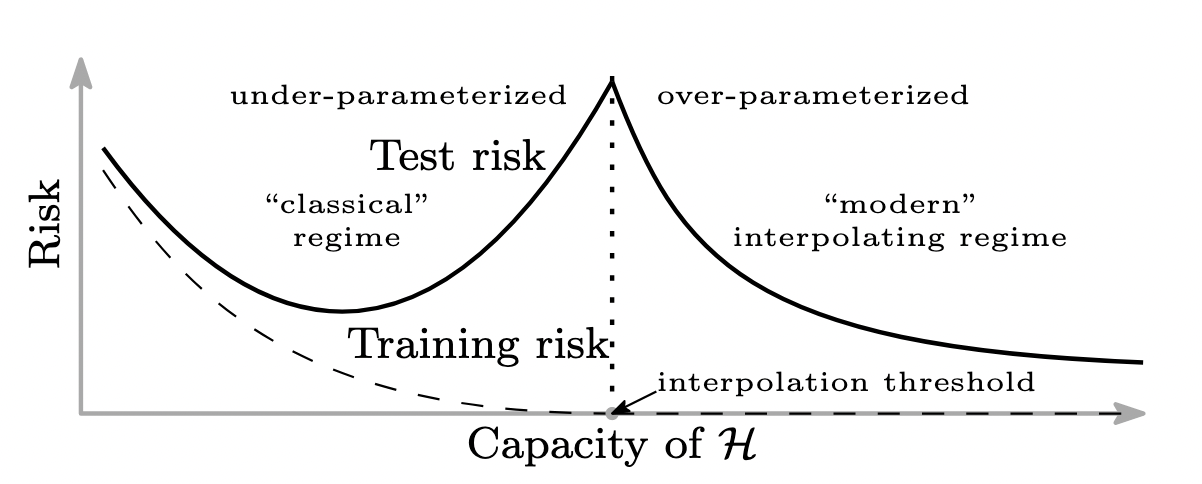
### Deep Double Descent: 2023
- A U-turn on Double Descent: Rethinking Parameter Counting in Statistical Learning. [[paper]](https://arxiv.org/abs/2310.18988)
- Alicia Curth, Alan Jeffares, Mihaela van der Schaar.
- Key Word: Deep Double Descent.
- Digest This paper challenges the conventional understanding of the relationship between model complexity and prediction error. It explores the phenomenon of "double descent," which suggests that test error can decrease as the parameter count exceeds the sample size. While this phenomenon has been observed in deep learning and other models like linear regression, trees, and boosting, the paper argues that the interpretation is influenced by multiple complexity axes. It demonstrates that the second descent occurs when the transition between these underlying axes happens and is not inherently tied to the interpolation threshold. The paper proposes a generalized measure for the effective number of parameters, which resolves tensions between double descent and traditional statistical intuition.
- Dropout Drops Double Descent. [[paper]](https://arxiv.org/abs/2305.16179)
- Tian-Le Yang, Joe Suzuki.
- Key Word: Dropout; Deep Double Descent.
- Digest The paper finds that adding a dropout layer before the fully-connected linear layer can drop the double descent phenomenon. Double descent is when the prediction error rises and drops as sample or model size increases. Optimal dropout can alleviate this in linear and nonlinear regression models, both theoretically and empirically. Optimal dropout can achieve a monotonic test error curve in nonlinear neural networks. Previous deep learning models do not encounter double-descent because they already apply regularization approaches like dropout.
- Double Descent Demystified: Identifying, Interpreting & Ablating the Sources of a Deep Learning Puzzle. [[paper]](https://arxiv.org/abs/2303.14151)
- Rylan Schaeffer, Mikail Khona, Zachary Robertson, Akhilan Boopathy, Kateryna Pistunova, Jason W. Rocks, Ila Rani Fiete, Oluwasanmi Koyejo.
- Key Word: Deep Double Descent; Tutorial.
- Digest We briefly describe double descent, then provide an explanation of why double descent occurs in an informal and approachable manner, requiring only familiarity with linear algebra and introductory probability. We provide visual intuition using polynomial regression, then mathematically analyze double descent with ordinary linear regression and identify three interpretable factors that, when simultaneously all present, together create double descent.
- Unifying Grokking and Double Descent. [[paper]](https://arxiv.org/abs/2303.06173) [[code]](https://github.com/xanderdavies/unifying-grok-dd)
- Xander Davies, Lauro Langosco, David Krueger.
- Key Word: Deep Double Descent; Grokking.
- Digest We hypothesize that grokking and double descent can be understood as instances of the same learning dynamics within a framework of pattern learning speeds. We propose that this framework also applies when varying model capacity instead of optimization steps, and provide the first demonstration of model-wise grokking.
### Deep Double Descent: 2022
- Sparse Double Descent: Where Network Pruning Aggravates Overfitting. [[paper]](https://arxiv.org/abs/2206.08684) [[code]](https://github.com/hezheug/sparse-double-descent)
- Zheng He, Zeke Xie, Quanzhi Zhu, Zengchang Qin. *ICML 2022*
- Key Word: Deep Double Descent; Lottery Ticket Hypothesis.
- Digest While recent studies focused on the deep double descent with respect to model overparameterization, they failed to recognize that sparsity may also cause double descent. In this paper, we have three main contributions. First, we report the novel sparse double descent phenomenon through extensive experiments. Second, for this phenomenon, we propose a novel learning distance interpretation that the curve of ℓ2 learning distance of sparse models (from initialized parameters to final parameters) may correlate with the sparse double descent curve well and reflect generalization better than minima flatness. Third, in the context of sparse double descent, a winning ticket in the lottery ticket hypothesis surprisingly may not always win.
- Can Neural Nets Learn the Same Model Twice? Investigating Reproducibility and Double Descent from the Decision Boundary Perspective. [[paper]](https://arxiv.org/abs/2203.08124) [[code]](https://github.com/somepago/dbviz)
- Gowthami Somepalli, Liam Fowl, Arpit Bansal, Ping Yeh-Chiang, Yehuda Dar, Richard Baraniuk, Micah Goldblum, Tom Goldstein. *CVPR 2022*
- Key Word: Deep Double Descent; Manifold.
- Digest We discuss methods for visualizing neural network decision boundaries and decision regions. We use these visualizations to investigate issues related to reproducibility and generalization in neural network training. We observe that changes in model architecture (and its associate inductive bias) cause visible changes in decision boundaries, while multiple runs with the same architecture yield results with strong similarities, especially in the case of wide architectures. We also use decision boundary methods to visualize double descent phenomena.
- Phenomenology of Double Descent in Finite-Width Neural Networks. [[paper]](https://arxiv.org/abs/2203.07337) [[code]](https://github.com/sidak/double-descent)
- Sidak Pal Singh, Aurelien Lucchi, Thomas Hofmann, Bernhard Schölkopf. *ICLR 2022*
- Key Word: Deep Double Descent.
- Digest 'Double descent' delineates the generalization behaviour of models depending on the regime they belong to: under- or over-parameterized. The current theoretical understanding behind the occurrence of this phenomenon is primarily based on linear and kernel regression models -- with informal parallels to neural networks via the Neural Tangent Kernel. Therefore such analyses do not adequately capture the mechanisms behind double descent in finite-width neural networks, as well as, disregard crucial components -- such as the choice of the loss function. We address these shortcomings by leveraging influence functions in order to derive suitable expressions of the population loss and its lower bound, while imposing minimal assumptions on the form of the parametric model.
### Deep Double Descent: 2021
- Multi-scale Feature Learning Dynamics: Insights for Double Descent. [[paper]](https://arxiv.org/abs/2112.03215) [[code]](https://github.com/nndoubledescent/doubledescent)
- Mohammad Pezeshki, Amartya Mitra, Yoshua Bengio, Guillaume Lajoie.
- Key Word: Deep Double Descent.
- Digest We investigate the origins of the less studied epoch-wise double descent in which the test error undergoes two non-monotonous transitions, or descents as the training time increases. By leveraging tools from statistical physics, we study a linear teacher-student setup exhibiting epoch-wise double descent similar to that in deep neural networks. In this setting, we derive closed-form analytical expressions for the evolution of generalization error over training. We find that double descent can be attributed to distinct features being learned at different scales: as fast-learning features overfit, slower-learning features start to fit, resulting in a second descent in test error.
- Asymptotic Risk of Overparameterized Likelihood Models: Double Descent Theory for Deep Neural Networks. [[paper]](https://arxiv.org/abs/2103.00500)
- Ryumei Nakada, Masaaki Imaizumi.
- Key Word: Deep Double Descent.
- Digest We consider a likelihood maximization problem without the model constraints and analyze the upper bound of an asymptotic risk of an estimator with penalization. Technically, we combine a property of the Fisher information matrix with an extended Marchenko-Pastur law and associate the combination with empirical process techniques. The derived bound is general, as it describes both the double descent and the regularized risk curves, depending on the penalization.
- Distilling Double Descent. [[paper]](https://arxiv.org/abs/2102.06849)
- Andrew Cotter, Aditya Krishna Menon, Harikrishna Narasimhan, Ankit Singh Rawat, Sashank J. Reddi, Yichen Zhou.
- Key Word: Deep Double Descent; Distillation.
- Digest Distillation is the technique of training a "student" model based on examples that are labeled by a separate "teacher" model, which itself is trained on a labeled dataset. The most common explanations for why distillation "works" are predicated on the assumption that student is provided with soft labels, e.g. probabilities or confidences, from the teacher model. In this work, we show, that, even when the teacher model is highly overparameterized, and provides hard labels, using a very large held-out unlabeled dataset to train the student model can result in a model that outperforms more "traditional" approaches.
### Deep Double Descent: 2020
- Understanding Double Descent Requires a Fine-Grained Bias-Variance Decomposition. [[paper]](https://arxiv.org/abs/2011.03321)
- Ben Adlam, Jeffrey Pennington. *NeurIPS 2020*
- Key Word: Deep Double Descent; Bias-Variance.
- Digest Classical learning theory suggests that the optimal generalization performance of a machine learning model should occur at an intermediate model complexity, with simpler models exhibiting high bias and more complex models exhibiting high variance of the predictive function. However, such a simple trade-off does not adequately describe deep learning models that simultaneously attain low bias and variance in the heavily overparameterized regime. A primary obstacle in explaining this behavior is that deep learning algorithms typically involve multiple sources of randomness whose individual contributions are not visible in the total variance. To enable fine-grained analysis, we describe an interpretable, symmetric decomposition of the variance into terms associated with the randomness from sampling, initialization, and the labels.
- Gradient Flow in Sparse Neural Networks and How Lottery Tickets Win. [[paper]](https://arxiv.org/abs/2010.03533) [[code]](https://github.com/google-research/rigl)
- Utku Evci, Yani A. Ioannou, Cem Keskin, Yann Dauphin. *AAAI 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest Sparse Neural Networks (NNs) can match the generalization of dense NNs using a fraction of the compute/storage for inference, and also have the potential to enable efficient training. However, naively training unstructured sparse NNs from random initialization results in significantly worse generalization, with the notable exceptions of Lottery Tickets (LTs) and Dynamic Sparse Training (DST). Through our analysis of gradient flow during training we attempt to answer: (1) why training unstructured sparse networks from random initialization performs poorly and; (2) what makes LTs and DST the exceptions?
- Multiple Descent: Design Your Own Generalization Curve. [[paper]](https://arxiv.org/abs/2008.01036)
- Lin Chen, Yifei Min, Mikhail Belkin, Amin Karbasi. *NeurIPS 2021*
- Key Word: Deep Double Descent.
- Digest This paper explores the generalization loss of linear regression in variably parameterized families of models, both under-parameterized and over-parameterized. We show that the generalization curve can have an arbitrary number of peaks, and moreover, locations of those peaks can be explicitly controlled. Our results highlight the fact that both classical U-shaped generalization curve and the recently observed double descent curve are not intrinsic properties of the model family. Instead, their emergence is due to the interaction between the properties of the data and the inductive biases of learning algorithms.
- Early Stopping in Deep Networks: Double Descent and How to Eliminate it. [[paper]](https://arxiv.org/abs/2007.10099) [[code]](https://github.com/MLI-lab/early_stopping_double_descent)
- Reinhard Heckel, Fatih Furkan Yilmaz. *ICLR 2021*
- Key Word: Deep Double Descent; Early Stopping.
- Digest We show that such epoch-wise double descent arises for a different reason: It is caused by a superposition of two or more bias-variance tradeoffs that arise because different parts of the network are learned at different epochs, and eliminating this by proper scaling of stepsizes can significantly improve the early stopping performance. We show this analytically for i) linear regression, where differently scaled features give rise to a superposition of bias-variance tradeoffs, and for ii) a two-layer neural network, where the first and second layer each govern a bias-variance tradeoff. Inspired by this theory, we study two standard convolutional networks empirically and show that eliminating epoch-wise double descent through adjusting stepsizes of different layers improves the early stopping performance significantly.
- Triple descent and the two kinds of overfitting: Where & why do they appear? [[paper]](https://arxiv.org/abs/2006.03509) [[code]](https://github.com/sdascoli/triple-descent-paper)
- Stéphane d'Ascoli, Levent Sagun, Giulio Biroli.
- Key Word:Deep Double Descent.
- Digest In this paper, we show that despite their apparent similarity, these two scenarios are inherently different. In fact, both peaks can co-exist when neural networks are applied to noisy regression tasks. The relative size of the peaks is governed by the degree of nonlinearity of the activation function. Building on recent developments in the analysis of random feature models, we provide a theoretical ground for this sample-wise triple descent.
- A Brief Prehistory of Double Descent. [[paper]](https://arxiv.org/abs/2004.04328)
- Marco Loog, Tom Viering, Alexander Mey, Jesse H. Krijthe, David M.J. Tax.
- Key Word: Deep Double Descent.
- Digest This letter draws attention to some original, earlier findings, of interest to double descent.
- Double Trouble in Double Descent : Bias and Variance(s) in the Lazy Regime. [[paper]](https://arxiv.org/abs/2003.01054) [[code]](https://github.com/lightonai/double-trouble-in-double-descent)
- Stéphane d'Ascoli, Maria Refinetti, Giulio Biroli, Florent Krzakala. *ICML 2020*
- Key Word: Deep Double Descent; Bias-Variance.
- Digest Deep neural networks can achieve remarkable generalization performances while interpolating the training data perfectly. Rather than the U-curve emblematic of the bias-variance trade-off, their test error often follows a "double descent" - a mark of the beneficial role of overparametrization. In this work, we develop a quantitative theory for this phenomenon in the so-called lazy learning regime of neural networks, by considering the problem of learning a high-dimensional function with random features regression. We obtain a precise asymptotic expression for the bias-variance decomposition of the test error, and show that the bias displays a phase transition at the interpolation threshold, beyond which it remains constant.
- Rethinking Bias-Variance Trade-off for Generalization of Neural Networks. [[paper]](https://arxiv.org/abs/2002.11328) [[code]](https://github.com/yaodongyu/Rethink-BiasVariance-Tradeoff)
- Zitong Yang, Yaodong Yu, Chong You, Jacob Steinhardt, Yi Ma. *ICML 2020*
- Key Word: Deep Double Descent; Bias-Variance.
- Digest The classical bias-variance trade-off predicts that bias decreases and variance increase with model complexity, leading to a U-shaped risk curve. Recent work calls this into question for neural networks and other over-parameterized models, for which it is often observed that larger models generalize better. We provide a simple explanation for this by measuring the bias and variance of neural networks: while the bias is monotonically decreasing as in the classical theory, the variance is unimodal or bell-shaped: it increases then decreases with the width of the network.
- The Curious Case of Adversarially Robust Models: More Data Can Help, Double Descend, or Hurt Generalization. [[paper]](https://arxiv.org/abs/2002.11080)
- Yifei Min, Lin Chen, Amin Karbasi. *UAI 2021*
- Key Word: Deep Double Descent.
- Digest We challenge this conventional belief and show that more training data can hurt the generalization of adversarially robust models in the classification problems. We first investigate the Gaussian mixture classification with a linear loss and identify three regimes based on the strength of the adversary. In the weak adversary regime, more data improves the generalization of adversarially robust models. In the medium adversary regime, with more training data, the generalization loss exhibits a double descent curve, which implies the existence of an intermediate stage where more training data hurts the generalization. In the strong adversary regime, more data almost immediately causes the generalization error to increase.
### Deep Double Descent: 2019
- Deep Double Descent: Where Bigger Models and More Data Hurt. [[paper]](https://arxiv.org/abs/1912.02292)
- Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever. *ICLR 2020*
- Key Word: Deep Double Descent.
- Digest We show that a variety of modern deep learning tasks exhibit a "double-descent" phenomenon where, as we increase model size, performance first gets worse and then gets better.
### Deep Double Descent: 2018
- Reconciling modern machine learning practice and the bias-variance trade-off. [[paper]](https://arxiv.org/abs/1812.11118)
- Mikhail Belkin, Daniel Hsu, Siyuan Ma, Soumik Mandal. *PNAS*
- Key Word: Bias-Variance; Over-Parameterization.
- Digest In this paper, we reconcile the classical understanding and the modern practice within a unified performance curve. This "double descent" curve subsumes the textbook U-shaped bias-variance trade-off curve by showing how increasing model capacity beyond the point of interpolation results in improved performance.
- A Modern Take on the Bias-Variance Tradeoff in Neural Networks. [[paper]](https://arxiv.org/abs/1810.08591)
- Brady Neal, Sarthak Mittal, Aristide Baratin, Vinayak Tantia, Matthew Scicluna, Simon Lacoste-Julien, Ioannis Mitliagkas.
- Key Word: Bias-Variance; Over-Parameterization.
- Digest The bias-variance tradeoff tells us that as model complexity increases, bias falls and variances increases, leading to a U-shaped test error curve. However, recent empirical results with over-parameterized neural networks are marked by a striking absence of the classic U-shaped test error curve: test error keeps decreasing in wider networks. Motivated by the shaky evidence used to support this claim in neural networks, we measure bias and variance in the modern setting. We find that both bias and variance can decrease as the number of parameters grows. To better understand this, we introduce a new decomposition of the variance to disentangle the effects of optimization and data sampling.
## Lottery Ticket Hypothesis
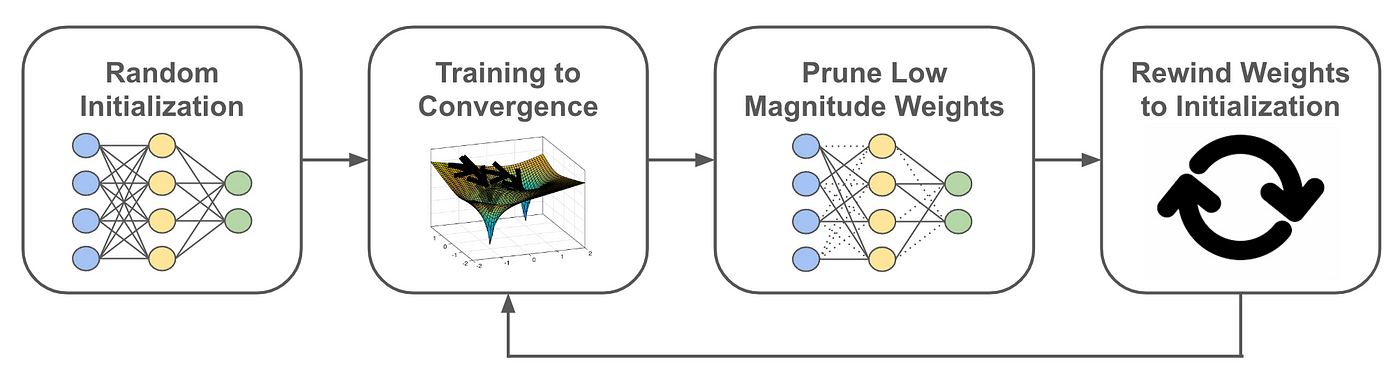
### Lottery Ticket Hypothesis: 2024
- On the Sparsity of the Strong Lottery Ticket Hypothesis.
- Emanuele Natale, Davide Ferré, Giordano Giambartolomei, Frédéric Giroire, Frederik Mallmann-Trenn.
- Key Word: Strong Lottery Ticket Hypothesis.
- Digest Recent research has explored the Strong Lottery Ticket Hypothesis (SLTH), which suggests that a random neural network contains subnetworks that can approximate smaller networks without training. This builds on the weaker Lottery Ticket Hypothesis, which states that large networks contain sparse subnetworks that can be efficiently trained to perform as well as the full network. However, previous SLTH results lacked guarantees on subnetwork size due to reliance on the Random Subset Sum (RSS) Problem. This paper provides the first proof of SLTH with subnetwork sparsity guarantees in settings like dense and equivariant networks. The key contribution is an improved bound on a variant of the RSS Problem, offering new insights into subnetwork size constraints.
- No Free Prune: Information-Theoretic Barriers to Pruning at Initialization. [[paper]](https://arxiv.org/abs/2402.01089)
- Tanishq Kumar, Kevin Luo, Mark Sellke.
- Key Word: Lottery Ticket Hypothesis; Overparameterization; Mutual Information.
- Digest This paper investigates the concept of "lottery tickets" in deep learning, questioning the necessity of large models versus identifying and training sparse networks from the start. Despite attempts, finding these efficient subnetworks without training the full model has largely failed. The study proposes a theoretical reason for this, focusing on the effective parameter count, which includes non-zero weights and the data-related information within the sparsity mask. It extends the Law of Robustness to sparse networks, suggesting that data-dependent masks are crucial for robust performance. The findings indicate that masks created during or after training contain more information than those at initialization, affecting the network's effective capacity. This explains the difficulty in finding lottery tickets without full model training, as confirmed by experimental results on neural networks.
### Lottery Ticket Hypothesis: 2023
- Instant Soup: Cheap Pruning Ensembles in A Single Pass Can Draw Lottery Tickets from Large Models. [[paper]](https://arxiv.org/abs/2306.10460)
- Ajay Jaiswal, Shiwei Liu, Tianlong Chen, Ying Ding, Zhangyang Wang.
- Key Word: Lottery Tickets; Model Soup.
- Digest The paper introduces Instant Soup Pruning (ISP), a novel approach that leverages the idea of model soups to generate high-quality subnetworks from large pre-trained models, reducing the computational cost compared to traditional iterative magnitude pruning (IMP) methods.
- A Three-regime Model of Network Pruning. [[paper]](https://arxiv.org/abs/2305.18383)
- Yefan Zhou, Yaoqing Yang, Arin Chang, Michael W. Mahoney.
- Key Word: Pruning; Linear Mode Connectivity.
- Digest This paper proposes a model based on statistical mechanics to predict how training hyperparameters affect pruning performance of neural networks. The paper finds a sharp transition phenomenon that depends on two parameters in the pre-pruned and pruned models. The paper also identifies three types of global structures in the pruned loss landscape and applies the model to three practical scenarios.
- Generalization Bounds for Magnitude-Based Pruning via Sparse Matrix Sketching. [[paper]](https://arxiv.org/abs/2305.18789)
- Etash Kumar Guha, Prasanjit Dubey, Xiaoming Huo.
- Key Word: Magnitude-Based Pruning; Norm-based Generalization Bound; Sparse Matrix Sketching.
- Digest This paper proposes a new bound on the generalization error of Magnitude-Based pruning1, a technique that removes weights with small magnitudes from neural networks. The paper improves on previous bounds by using Sparse Matrix Sketching, a method that compresses pruned matrices into smaller dimensions. The paper also extends the results to Iterative Pruning, a process that prunes and retrains the network multiple times. The paper shows that the new method achieves better generalization than existing methods on some datasets.
- Pruning at Initialization -- A Sketching Perspective. [[paper]](https://arxiv.org/abs/2305.17559)
- Noga Bar, Raja Giryes.
- Key Word: Pruning at Ininitialization; Sketching Algorithm; Neural Tangent Kernel.
- Digest The paper studies how to prune linear neural networks before training. They show that this problem is related to the sketching problem for fast matrix multiplication. They use this connection to analyze the error and data dependence of pruning at initialization. They also propose a general improvement to existing pruning algorithms based on sketching techniques.
- NTK-SAP: Improving neural network pruning by aligning training dynamics. [[paper]](https://arxiv.org/abs/2304.02840) [[code]](https://github.com/YiteWang/NTK-SAP)
- Yite Wang, Dawei Li, Ruoyu Sun. *ICLR 2023*
- Key Word: Pruning at Ininitialization; Neural Tangent Kernel.
- Digest We propose to prune the connections that have the least influence on the spectrum of the NTK. This method can help maintain the NTK spectrum, which may help align the training dynamics to that of its dense counterpart. However, one possible issue is that the fixed-weight-NTK corresponding to a given initial point can be very different from the NTK corresponding to later iterates during the training phase.
- Sparsity May Cry: Let Us Fail (Current) Sparse Neural Networks Together! [[paper]](https://arxiv.org/abs/2303.02141) [[code]](https://github.com/VITA-Group/SMC-Bench)
- Shiwei Liu, Tianlong Chen, Zhenyu Zhang, Xuxi Chen, Tianjin Huang, Ajay Jaiswal, Zhangyang Wang. *ICLR 2023*
- Key Word: Sparse Neural Network; Benchmark.
- Digest In absence of a carefully crafted evaluation benchmark, most if not all, sparse algorithms are evaluated against fairly simple and naive tasks (eg. CIFAR, ImageNet, GLUE, etc.), which can potentially camouflage many advantages as well unexpected predicaments of SNNs. In pursuit of a more general evaluation and unveiling the true potential of sparse algorithms, we introduce "Sparsity May Cry" Benchmark (SMC-Bench), a collection of carefully-curated 4 diverse tasks with 10 datasets, that accounts for capturing a wide range of domain-specific and sophisticated knowledge.
- Pruning Deep Neural Networks from a Sparsity Perspective. [[paper]](https://arxiv.org/abs/2302.05601) [[code]](https://github.com/dem123456789/Pruning-Deep-Neural-Networks-from-a-Sparsity-Perspective)
- Enmao Diao, Ganghua Wang, Jiawei Zhan, Yuhong Yang, Jie Ding, Vahid Tarokh. *ICLR 2023*
- Key Word: Theory of Model Compression; Sparsity Measure.
- Digest Many deep pruning algorithms have been proposed with impressive empirical success. However, existing approaches lack a quantifiable measure to estimate the compressibility of a sub-network during each pruning iteration and thus may under-prune or over-prune the model. In this work, we propose PQ Index (PQI) to measure the potential compressibility of deep neural networks and use this to develop a Sparsity-informed Adaptive Pruning (SAP) algorithm.
- Why is the State of Neural Network Pruning so Confusing? On the Fairness, Comparison Setup, and Trainability in Network Pruning. [[paper]](https://arxiv.org/abs/2301.05219) [[code]](https://github.com/mingsun-tse/why-the-state-of-pruning-so-confusing)
- Huan Wang, Can Qin, Yue Bai, Yun Fu.
- Key Word: Pruning; Empirical Study.
- Digest Two mysteries in pruning represent such a confusing status: the performance-boosting effect of a larger finetuning learning rate, and the no-value argument of inheriting pretrained weights in filter pruning. In this work, we attempt to explain the confusing state of network pruning by demystifying the two mysteries.
- Theoretical Characterization of How Neural Network Pruning Affects its Generalization. [[paper]](https://arxiv.org/abs/2301.00335)
- Hongru Yang, Yingbin Liang, Xiaojie Guo, Lingfei Wu, Zhangyang Wang.
- Key Word: Lottery Ticket Hypothesis; Generalization Bound.
- Digest This work considers a classification task for overparameterized two-layer neural networks, where the network is randomly pruned according to different rates at the initialization. It is shown that as long as the pruning fraction is below a certain threshold, gradient descent can drive the training loss toward zero and the network exhibits good generalization performance. More surprisingly, the generalization bound gets better as the pruning fraction gets larger.
### Lottery Ticket Hypothesis: 2022
- Revisit Kernel Pruning with Lottery Regulated Grouped Convolutions. [[paper]](https://openreview.net/forum?id=LdEhiMG9WLO) [[code]](https://github.com/choH/lottery_regulated_grouped_kernel_pruning)
- Shaochen Zhong, Guanqun Zhang, Ningjia Huang, Shuai Xu. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis.
- Digest We revisit the idea of kernel pruning, a heavily overlooked approach under the context of structured pruning. This is because kernel pruning will naturally introduce sparsity to filters within the same convolutional layer — thus, making the remaining network no longer dense. We address this problem by proposing a versatile grouped pruning framework where we first cluster filters from each convolutional layer into equal-sized groups, prune the grouped kernels we deem unimportant from each filter group, then permute the remaining filters to form a densely grouped convolutional architecture (which also enables the parallel computing capability) for fine-tuning.
- Proving the Lottery Ticket Hypothesis for Convolutional Neural Networks. [[paper]](https://openreview.net/forum?id=Vjki79-619-)
- Arthur da Cunha, Emanuele Natale, Laurent Viennot, Laurent_Viennot. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent theoretical works proved an even stronger version: every sufficiently overparameterized (dense) neural network contains a subnetwork that, even without training, achieves accuracy comparable to that of the trained large network. These works left as an open problem to extend the result to convolutional neural networks (CNNs). In this work we provide such generalization by showing that, with high probability, it is possible to approximate any CNN by pruning a random CNN whose size is larger by a logarithmic factor.
- Audio Lottery: Speech Recognition Made Ultra-Lightweight, Noise-Robust, and Transferable. [[paper]](https://openreview.net/forum?id=9Nk6AJkVYB) [[code]](https://github.com/VITA-Group/Audio-Lottery)
- Shaojin Ding, Tianlong Chen, Zhangyang Wang. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis; Speech Recognition.
- Digest We investigate the tantalizing possibility of using lottery ticket hypothesis to discover lightweight speech recognition models, that are (1) robust to various noise existing in speech; (2) transferable to fit the open-world personalization; and 3) compatible with structured sparsity.
- Strong Lottery Ticket Hypothesis with ε--perturbation. [[paper]](https://arxiv.org/abs/2210.16589)
- Zheyang Xiong, Fangshuo Liao, Anastasios Kyrillidis.
- Key Word: Lottery Ticket Hypothesis.
- Digest The strong Lottery Ticket Hypothesis (LTH) claims the existence of a subnetwork in a sufficiently large, randomly initialized neural network that approximates some target neural network without the need of training. We extend the theoretical guarantee of the strong LTH literature to a scenario more similar to the original LTH, by generalizing the weight change in the pre-training step to some perturbation around initialization.
- Large Models are Parsimonious Learners: Activation Sparsity in Trained Transformers. [[paper]](https://arxiv.org/abs/2210.06313)
- Zonglin Li, Chong You, Srinadh Bhojanapalli, Daliang Li, Ankit Singh Rawat, Sashank J. Reddi, Ke Ye, Felix Chern, Felix Yu, Ruiqi Guo, Sanjiv Kumar.
- Key Word: Sparse Activation; Large Models; Transformers.
- Digest This paper studies the curious phenomenon for machine learning models with Transformer architectures that their activation maps are sparse. By activation map we refer to the intermediate output of the multi-layer perceptrons (MLPs) after a ReLU activation function, and by "sparse" we mean that on average very few entries (e.g., 3.0% for T5-Base and 6.3% for ViT-B16) are nonzero for each input to MLP.
- Unmasking the Lottery Ticket Hypothesis: What's Encoded in a Winning Ticket's Mask? [[paper]](https://arxiv.org/abs/2210.03044)
- Mansheej Paul, Feng Chen, Brett W. Larsen, Jonathan Frankle, Surya Ganguli, Gintare Karolina Dziugaite.
- Key Word: Lottery Ticket Hypothesis; Mode Connectivity.
- Digest First, we find that—at higher sparsities—pairs of pruned networks at successive pruning iterations are connected by a linear path with zero error barrier if and only if they are matching. This indicates that masks found at the end of training convey the identity of an axial subspace that intersects a desired linearly connected mode of a matching sublevel set. Second, we show SGD can exploit this information due to a strong form of robustness: it can return to this mode despite strong perturbations early in training. Third, we show how the flatness of the error landscape at the end of training determines a limit on the fraction of weights that can be pruned at each iteration of IMP. Finally, we show that the role of retraining in IMP is to find a network with new small weights to prune.
- How Erdös and Rényi Win the Lottery. [[paper]](https://arxiv.org/abs/2210.02412)
- Advait Gadhikar, Sohum Mukherjee, Rebekka Burkholz.
- Key Word: Lottery Ticket Hypothesis; Erdös-Rényi Random Graphs.
- Digest Random masks define surprisingly effective sparse neural network models, as has been shown empirically. The resulting Erdös-Rényi (ER) random graphs can often compete with dense architectures and state-of-the-art lottery ticket pruning algorithms struggle to outperform them, even though the random baselines do not rely on computationally expensive pruning-training iterations but can be drawn initially without significant computational overhead. We offer a theoretical explanation of how such ER masks can approximate arbitrary target networks if they are wider by a logarithmic factor in the inverse sparsity 1/log(1/sparsity).
- SparCL: Sparse Continual Learning on the Edge. [[paper]](https://arxiv.org/abs/2209.09476)
- Zifeng Wang, Zheng Zhan, Yifan Gong, Geng Yuan, Wei Niu, Tong Jian, Bin Ren, Stratis Ioannidis, Yanzhi Wang, Jennifer Dy. *NeurIPS 2022*
- Key Word: Continual Learning; Sparse Training.
- Digest We propose a novel framework called Sparse Continual Learning(SparCL), which is the first study that leverages sparsity to enable cost-effective continual learning on edge devices. SparCL achieves both training acceleration and accuracy preservation through the synergy of three aspects: weight sparsity, data efficiency, and gradient sparsity. Specifically, we propose task-aware dynamic masking (TDM) to learn a sparse network throughout the entire CL process, dynamic data removal (DDR) to remove less informative training data, and dynamic gradient masking (DGM) to sparsify the gradient updates.
- One-shot Network Pruning at Initialization with Discriminative Image Patches. [[paper]](https://arxiv.org/abs/2209.05683)
- Yinan Yang, Ying Ji, Yu Wang, Heng Qi, Jien Kato.
- Key Word: One-Shot Network Pruning.
- Digest We propose two novel methods, Discriminative One-shot Network Pruning (DOP) and Super Stitching, to prune the network by high-level visual discriminative image patches. Our contributions are as follows. (1) Extensive experiments reveal that OPaI is data-dependent. (2) Super Stitching performs significantly better than the original OPaI method on benchmark ImageNet, especially in a highly compressed model.
- SuperTickets: Drawing Task-Agnostic Lottery Tickets from Supernets via Jointly Architecture Searching and Parameter Pruning. [[paper]](https://arxiv.org/abs/2207.03677) [[code]](https://github.com/RICE-EIC/SuperTickets)
- Haoran You, Baopu Li, Zhanyi Sun, Xu Ouyang, Yingyan Lin. *ECCV 2022*
- Key Word: Lottery Ticket Hypothesis; Neural Architecture Search.
- Digest We discover for the first time that both efficient DNNs and their lottery subnetworks (i.e., lottery tickets) can be directly identified from a supernet, which we term as SuperTickets, via a two-in-one training scheme with jointly architecture searching and parameter pruning. Moreover, we develop a progressive and unified SuperTickets identification strategy that allows the connectivity of subnetworks to change during supernet training, achieving better accuracy and efficiency trade-offs than conventional sparse training.
- Lottery Ticket Hypothesis for Spiking Neural Networks. [[paper]](https://arxiv.org/abs/2207.01382)
- Youngeun Kim, Yuhang Li, Hyoungseob Park, Yeshwanth Venkatesha, Ruokai Yin, Priyadarshini Panda. *ECCV 2022*
- Key Word: Lottery Ticket Hypothesis; Spiking Neural Networks.
- Digest Spiking Neural Networks (SNNs) have recently emerged as a new generation of low-power deep neural networks where binary spikes convey information across multiple timesteps. Pruning for SNNs is highly important as they become deployed on a resource-constraint mobile/edge device. The previous SNN pruning works focus on shallow SNNs (2~6 layers), however, deeper SNNs (>16 layers) are proposed by state-of-the-art SNN works, which is difficult to be compatible with the current pruning work. To scale up a pruning technique toward deep SNNs, we investigate Lottery Ticket Hypothesis (LTH) which states that dense networks contain smaller subnetworks (i.e., winning tickets) that achieve comparable performance to the dense networks. Our studies on LTH reveal that the winning tickets consistently exist in deep SNNs across various datasets and architectures, providing up to 97% sparsity without huge performance degradation.
- Winning the Lottery Ahead of Time: Efficient Early Network Pruning. [[paper]](https://arxiv.org/abs/2206.10451)
- John Rachwan, Daniel Zügner, Bertrand Charpentier, Simon Geisler, Morgane Ayle, Stephan Günnemann. *ICML 2022*
- Key Word: Lottery Ticket Hypothesis; Neural Tangent Kernel.
- Digest Although state-of-the-art pruning methods extract highly sparse models, they neglect two main challenges: (1) the process of finding these sparse models is often very expensive; (2) unstructured pruning does not provide benefits in terms of GPU memory, training time, or carbon emissions. We propose Early Compression via Gradient Flow Preservation (EarlyCroP), which efficiently extracts state-of-the-art sparse models before or early in training addressing challenge (1), and can be applied in a structured manner addressing challenge (2). This enables us to train sparse networks on commodity GPUs whose dense versions would be too large, thereby saving costs and reducing hardware requirements.
- "Understanding Robustness Lottery": A Comparative Visual Analysis of Neural Network Pruning Approaches. [[paper]](https://arxiv.org/abs/2206.07918)
- Zhimin Li, Shusen Liu, Xin Yu, Kailkhura Bhavya, Jie Cao, Diffenderfer James Daniel, Peer-Timo Bremer, Valerio Pascucci.
- Key Word: Lottery Ticket Hypothesis; Out-of-Distribution Generalization; Visualization.
- Digest This work aims to shed light on how different pruning methods alter the network's internal feature representation, and the corresponding impact on model performance. To provide a meaningful comparison and characterization of model feature space, we use three geometric metrics that are decomposed from the common adopted classification loss. With these metrics, we design a visualization system to highlight the impact of pruning on model prediction as well as the latent feature embedding.
- Data-Efficient Double-Win Lottery Tickets from Robust Pre-training. [[paper]](https://arxiv.org/abs/2206.04762) [[code]](https://github.com/VITA-Group/Double-Win-LTH)
- Tianlong Chen, Zhenyu Zhang, Sijia Liu, Yang Zhang, Shiyu Chang, Zhangyang Wang. *ICML 2022*
- Key Word: Lottery Ticket Hypothesis; Adversarial Training; Robust Pre-training.
- Digest We formulate a more rigorous concept, Double-Win Lottery Tickets, in which a located subnetwork from a pre-trained model can be independently transferred on diverse downstream tasks, to reach BOTH the same standard and robust generalization, under BOTH standard and adversarial training regimes, as the full pre-trained model can do. We comprehensively examine various pre-training mechanisms and find that robust pre-training tends to craft sparser double-win lottery tickets with superior performance over the standard counterparts.
- HideNseek: Federated Lottery Ticket via Server-side Pruning and Sign Supermask. [[paper]](https://arxiv.org/abs/2206.04385)
- Anish K. Vallapuram, Pengyuan Zhou, Young D. Kwon, Lik Hang Lee, Hengwei Xu, Pan Hui.
- Key Word: Lottery Ticket Hypothesis; Federated Learning.
- Digest We propose HideNseek which employs one-shot data-agnostic pruning at initialization to get a subnetwork based on weights' synaptic saliency. Each client then optimizes a sign supermask multiplied by the unpruned weights to allow faster convergence with the same compression rates as state-of-the-art.
- Lottery Tickets on a Data Diet: Finding Initializations with Sparse Trainable Networks. [[paper]](https://arxiv.org/abs/2206.01278) [[code]](https://github.com/mansheej/lth_diet)
- Mansheej Paul, Brett W. Larsen, Surya Ganguli, Jonathan Frankle, Gintare Karolina Dziugaite. *NeurIPS 2022*
- Key Word: Lottery Ticket Hypothesis; Pre-training.
- Digest We seek to understand how this early phase of pre-training leads to a good initialization for IMP both through the lens of the data distribution and the loss landscape geometry. Empirically we observe that, holding the number of pre-training iterations constant, training on a small fraction of (randomly chosen) data suffices to obtain an equally good initialization for IMP. We additionally observe that by pre-training only on "easy" training data, we can decrease the number of steps necessary to find a good initialization for IMP compared to training on the full dataset or a randomly chosen subset. Finally, we identify novel properties of the loss landscape of dense networks that are predictive of IMP performance, showing in particular that more examples being linearly mode connected in the dense network correlates well with good initializations for IMP.
- Analyzing Lottery Ticket Hypothesis from PAC-Bayesian Theory Perspective. [[paper]](https://arxiv.org/abs/2205.07320)
- Keitaro Sakamoto, Issei Sato. *NeurIPS 2022*
- Key Word: Lottery Ticket Hypothesis; PAC-Bayes.
- Digest We confirm this hypothesis and show that the PAC-Bayesian theory can provide an explicit understanding of the relationship between LTH and generalization behavior. On the basis of our experimental findings that flatness is useful for improving accuracy and robustness to label noise and that the distance from the initial weights is deeply involved in winning tickets, we offer the PAC-Bayes bound using a spike-and-slab distribution to analyze winning tickets.
- Dual Lottery Ticket Hypothesis. [[paper]](https://arxiv.org/abs/2203.04248) [[code]](https://github.com/yueb17/dlth)
- Yue Bai, Huan Wang, Zhiqiang Tao, Kunpeng Li, Yun Fu. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis.
- Digest This paper articulates a Dual Lottery Ticket Hypothesis (DLTH) as a dual format of original Lottery Ticket Hypothesis (LTH). Correspondingly, a simple regularization based sparse network training strategy, Random Sparse Network Transformation (RST), is proposed to validate DLTH and enhance sparse network training.
- Rare Gems: Finding Lottery Tickets at Initialization. [[paper]](https://arxiv.org/abs/2202.12002)
- Kartik Sreenivasan, Jy-yong Sohn, Liu Yang, Matthew Grinde, Alliot Nagle, Hongyi Wang, Eric Xing, Kangwook Lee, Dimitris Papailiopoulos. *NeurIPS 2022*
- Key Word: Lottery Ticket Hypothesis; Sanity Checks; Pruning at Initialization.
- Digest Finding lottery tickets that train to better accuracy compared to simple baselines remains an open problem. In this work, we resolve this open problem by proposing Gem-Miner which finds lottery tickets at initialization that beat current baselines. Gem-Miner finds lottery tickets trainable to accuracy competitive or better than Iterative Magnitude Pruning (IMP), and does so up to 19× faster.
- Reconstruction Task Finds Universal Winning Tickets. [[paper]](https://arxiv.org/abs/2202.11484)
- Ruichen Li, Binghui Li, Qi Qian, Liwei Wang.
- Key Word: Lottery Ticket Hypothesis; Self-Supervision.
- Digest We show that the image-level pretrain task is not capable of pruning models for diverse downstream tasks. To mitigate this problem, we introduce image reconstruction, a pixel-level task, into the traditional pruning framework. Concretely, an autoencoder is trained based on the original model, and then the pruning process is optimized with both autoencoder and classification losses.
- Finding Dynamics Preserving Adversarial Winning Tickets. [[paper]](https://arxiv.org/abs/2202.06488) [[code]](https://github.com/google/neural-tangents)
- Xupeng Shi, Pengfei Zheng, A. Adam Ding, Yuan Gao, Weizhong Zhang. *AISTATS 2022*
- Key Word: Lottery Ticket Hypothesis; Neural Tangent Kernel.
- Digest Based on recent works of Neural Tangent Kernel (NTK), we systematically study the dynamics of adversarial training and prove the existence of trainable sparse sub-network at initialization which can be trained to be adversarial robust from scratch. This theoretically verifies the lottery ticket hypothesis in adversarial context and we refer such sub-network structure as Adversarial Winning Ticket (AWT). We also show empirical evidences that AWT preserves the dynamics of adversarial training and achieve equal performance as dense adversarial training.
### Lottery Ticket Hypothesis: 2021
- Plant 'n' Seek: Can You Find the Winning Ticket? [[paper]](https://arxiv.org/abs/2111.11153) [[code]](https://github.com/RelationalML/PlantNSeek)
- Jonas Fischer, Rebekka Burkholz. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis.
- Digest Currently, such algorithms are primarily evaluated on imaging data, for which we lack ground truth information and thus the understanding of how sparse lottery tickets could be. To fill this gap, we develop a framework that allows us to plant and hide winning tickets with desirable properties in randomly initialized neural networks. To analyze the ability of state-of-the-art pruning to identify tickets of extreme sparsity, we design and hide such tickets solving four challenging tasks.
- On the Existence of Universal Lottery Tickets. [[paper]](https://arxiv.org/abs/2111.11146) [[code]](https://github.com/relationalml/universallt)
- Rebekka Burkholz, Nilanjana Laha, Rajarshi Mukherjee, Alkis Gotovos. *ICLR 2022*
- Key Word: Lottery Ticket Hypothesis.
- Digest The lottery ticket hypothesis conjectures the existence of sparse subnetworks of large randomly initialized deep neural networks that can be successfully trained in isolation. Recent work has experimentally observed that some of these tickets can be practically reused across a variety of tasks, hinting at some form of universality. We formalize this concept and theoretically prove that not only do such universal tickets exist but they also do not require further training.
- Universality of Winning Tickets: A Renormalization Group Perspective. [[paper]](https://arxiv.org/abs/2110.03210)
- William T. Redman, Tianlong Chen, Zhangyang Wang, Akshunna S. Dogra. *ICML 2022*
- Key Word: Lottery Ticket Hypothesis; Renormalization Group Theory.
- Digest Foundational work on the Lottery Ticket Hypothesis has suggested an exciting corollary: winning tickets found in the context of one task can be transferred to similar tasks, possibly even across different architectures. This has generated broad interest, but methods to study this universality are lacking. We make use of renormalization group theory, a powerful tool from theoretical physics, to address this need. We find that iterative magnitude pruning, the principal algorithm used for discovering winning tickets, is a renormalization group scheme, and can be viewed as inducing a flow in parameter space.
- How many degrees of freedom do we need to train deep networks: a loss landscape perspective. [[paper]](https://arxiv.org/abs/2107.05802) [[code]](https://github.com/ganguli-lab/degrees-of-freedom)
- Brett W. Larsen, Stanislav Fort, Nic Becker, Surya Ganguli. *ICLR 2022*
- Key Word: Loss Landscape; Lottery Ticket Hypothesis.
- Digest A variety of recent works, spanning pruning, lottery tickets, and training within random subspaces, have shown that deep neural networks can be trained using far fewer degrees of freedom than the total number of parameters. We analyze this phenomenon for random subspaces by first examining the success probability of hitting a training loss sublevel set when training within a random subspace of a given training dimensionality.
- A Winning Hand: Compressing Deep Networks Can Improve Out-Of-Distribution Robustness. [[paper]](https://arxiv.org/abs/2106.09129)
- James Diffenderfer, Brian R. Bartoldson, Shreya Chaganti, Jize Zhang, Bhavya Kailkhura. *NeurIPS 2021*
- Key Word: Lottery Ticket Hypothesis; Out-of-Distribution Generalization.
- Digest We perform a large-scale analysis of popular model compression techniques which uncovers several intriguing patterns. Notably, in contrast to traditional pruning approaches (e.g., fine tuning and gradual magnitude pruning), we find that "lottery ticket-style" approaches can surprisingly be used to produce CARDs, including binary-weight CARDs. Specifically, we are able to create extremely compact CARDs that, compared to their larger counterparts, have similar test accuracy and matching (or better) robustness -- simply by pruning and (optionally) quantizing.
- Efficient Lottery Ticket Finding: Less Data is More. [[paper]](https://arxiv.org/abs/2106.03225) [[code]](https://github.com/VITA-Group/PrAC-LTH)
- Zhenyu Zhang, Xuxi Chen, Tianlong Chen, Zhangyang Wang. *ICML 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest This paper explores a new perspective on finding lottery tickets more efficiently, by doing so only with a specially selected subset of data, called Pruning-Aware Critical set (PrAC set), rather than using the full training set. The concept of PrAC set was inspired by the recent observation, that deep networks have samples that are either hard to memorize during training, or easy to forget during pruning.
- A Probabilistic Approach to Neural Network Pruning. [[paper]](https://arxiv.org/abs/2105.10065)
- Xin Qian, Diego Klabjan. *ICML 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest We theoretically study the performance of two pruning techniques (random and magnitude-based) on FCNs and CNNs. Given a target network whose weights are independently sampled from appropriate distributions, we provide a universal approach to bound the gap between a pruned and the target network in a probabilistic sense. The results establish that there exist pruned networks with expressive power within any specified bound from the target network.
- On Lottery Tickets and Minimal Task Representations in Deep Reinforcement Learning. [[paper]](https://arxiv.org/abs/2105.01648)
- Marc Aurel Vischer, Robert Tjarko Lange, Henning Sprekeler. *ICLR 2022*
- Key Word: Reinforcement Learning; Lottery Ticket Hypothesis.
- Digest The lottery ticket hypothesis questions the role of overparameterization in supervised deep learning. But how is the performance of winning lottery tickets affected by the distributional shift inherent to reinforcement learning problems? In this work, we address this question by comparing sparse agents who have to address the non-stationarity of the exploration-exploitation problem with supervised agents trained to imitate an expert. We show that feed-forward networks trained with behavioural cloning compared to reinforcement learning can be pruned to higher levels of sparsity without performance degradation.
- Multi-Prize Lottery Ticket Hypothesis: Finding Accurate Binary Neural Networks by Pruning A Randomly Weighted Network. [[paper]](https://arxiv.org/abs/2103.09377) [[code]](https://github.com/chrundle/biprop)
- James Diffenderfer, Bhavya Kailkhura. *ICLR 2021*
- Key Word: Lottery Ticket Hypothesis; Binary Neural Networks.
- Digest This provides a new paradigm for learning compact yet highly accurate binary neural networks simply by pruning and quantizing randomly weighted full precision neural networks. We also propose an algorithm for finding multi-prize tickets (MPTs) and test it by performing a series of experiments on CIFAR-10 and ImageNet datasets. Empirical results indicate that as models grow deeper and wider, multi-prize tickets start to reach similar (and sometimes even higher) test accuracy compared to their significantly larger and full-precision counterparts that have been weight-trained.
- Do We Actually Need Dense Over-Parameterization? In-Time Over-Parameterization in Sparse Training. [[paper]](https://arxiv.org/abs/2102.02887) [[code]](https://github.com/Shiweiliuiiiiiii/In-Time-Over-Parameterization)
- Shiwei Liu, Lu Yin, Decebal Constantin Mocanu, Mykola Pechenizkiy. *ICML 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest In this paper, we introduce a new perspective on training deep neural networks capable of state-of-the-art performance without the need for the expensive over-parameterization by proposing the concept of In-Time Over-Parameterization (ITOP) in sparse training. By starting from a random sparse network and continuously exploring sparse connectivities during training, we can perform an Over-Parameterization in the space-time manifold, closing the gap in the expressibility between sparse training and dense training.
- Sparsity in Deep Learning: Pruning and growth for efficient inference and training in neural networks. [[paper]](https://arxiv.org/abs/2102.00554)
- Torsten Hoefler, Dan Alistarh, Tal Ben-Nun, Nikoli Dryden, Alexandra Peste.
- Key Word: Sparsity; Survey.
- Digest We survey prior work on sparsity in deep learning and provide an extensive tutorial of sparsification for both inference and training. We describe approaches to remove and add elements of neural networks, different training strategies to achieve model sparsity, and mechanisms to exploit sparsity in practice. Our work distills ideas from more than 300 research papers and provides guidance to practitioners who wish to utilize sparsity today, as well as to researchers whose goal is to push the frontier forward.
- A Unified Paths Perspective for Pruning at Initialization. [[paper]](https://arxiv.org/abs/2101.10552)
- Thomas Gebhart, Udit Saxena, Paul Schrater.
- Key Word: Lottery Ticket Hypothesis; Neural Tangent Kernel.
- Digest Leveraging recent theoretical approximations provided by the Neural Tangent Kernel, we unify a number of popular approaches for pruning at initialization under a single path-centric framework. We introduce the Path Kernel as the data-independent factor in a decomposition of the Neural Tangent Kernel and show the global structure of the Path Kernel can be computed efficiently. This Path Kernel decomposition separates the architectural effects from the data-dependent effects within the Neural Tangent Kernel, providing a means to predict the convergence dynamics of a network from its architecture alone.
### Lottery Ticket Hypothesis: 2020
- PHEW: Constructing Sparse Networks that Learn Fast and Generalize Well without Training Data. [[paper]](https://arxiv.org/abs/2010.11354) [[code]](https://github.com/ShreyasMalakarjunPatil/PHEW)
- Shreyas Malakarjun Patil, Constantine Dovrolis. *ICLR 2021*
- Key Word: Lottery Ticket Hypothesis; Neural Tangent Kernel.
- Digest Our work is based on a recently proposed decomposition of the Neural Tangent Kernel (NTK) that has decoupled the dynamics of the training process into a data-dependent component and an architecture-dependent kernel - the latter referred to as Path Kernel. That work has shown how to design sparse neural networks for faster convergence, without any training data, using the Synflow-L2 algorithm. We first show that even though Synflow-L2 is optimal in terms of convergence, for a given network density, it results in sub-networks with "bottleneck" (narrow) layers - leading to poor performance as compared to other data-agnostic methods that use the same number of parameters.
- A Gradient Flow Framework For Analyzing Network Pruning. [[paper]](https://arxiv.org/abs/2009.11839) [[code]](https://github.com/EkdeepSLubana/flowandprune)
- Ekdeep Singh Lubana, Robert P. Dick. *ICLR 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent network pruning methods focus on pruning models early-on in training. To estimate the impact of removing a parameter, these methods use importance measures that were originally designed to prune trained models. Despite lacking justification for their use early-on in training, such measures result in surprisingly low accuracy loss. To better explain this behavior, we develop a general framework that uses gradient flow to unify state-of-the-art importance measures through the norm of model parameters.
- Sanity-Checking Pruning Methods: Random Tickets can Win the Jackpot. [[paper]](https://arxiv.org/abs/2009.11094) [[code]](https://github.com/JingtongSu/sanity-checking-pruning)
- Jingtong Su, Yihang Chen, Tianle Cai, Tianhao Wu, Ruiqi Gao, Liwei Wang, Jason D. Lee. *NeurIPS 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We conduct sanity checks for the above beliefs on several recent unstructured pruning methods and surprisingly find that: (1) A set of methods which aims to find good subnetworks of the randomly-initialized network (which we call "initial tickets"), hardly exploits any information from the training data; (2) For the pruned networks obtained by these methods, randomly changing the preserved weights in each layer, while keeping the total number of preserved weights unchanged per layer, does not affect the final performance.
- Pruning Neural Networks at Initialization: Why are We Missing the Mark? [[paper]](https://arxiv.org/abs/2009.08576)
- Jonathan Frankle, Gintare Karolina Dziugaite, Daniel M. Roy, Michael Carbin. *ICLR 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent work has explored the possibility of pruning neural networks at initialization. We assess proposals for doing so: SNIP (Lee et al., 2019), GraSP (Wang et al., 2020), SynFlow (Tanaka et al., 2020), and magnitude pruning. Although these methods surpass the trivial baseline of random pruning, they remain below the accuracy of magnitude pruning after training, and we endeavor to understand why. We show that, unlike pruning after training, randomly shuffling the weights these methods prune within each layer or sampling new initial values preserves or improves accuracy. As such, the per-weight pruning decisions made by these methods can be replaced by a per-layer choice of the fraction of weights to prune. This property suggests broader challenges with the underlying pruning heuristics, the desire to prune at initialization, or both.
- ESPN: Extremely Sparse Pruned Networks. [[paper]](https://arxiv.org/abs/2006.15741) [[code]](https://github.com/chomd90/extreme_sparse)
- Minsu Cho, Ameya Joshi, Chinmay Hegde.
- Key Word: Lottery Ticket Hypothesis.
- Digest Deep neural networks are often highly overparameterized, prohibiting their use in compute-limited systems. However, a line of recent works has shown that the size of deep networks can be considerably reduced by identifying a subset of neuron indicators (or mask) that correspond to significant weights prior to training. We demonstrate that an simple iterative mask discovery method can achieve state-of-the-art compression of very deep networks. Our algorithm represents a hybrid approach between single shot network pruning methods (such as SNIP) with Lottery-Ticket type approaches. We validate our approach on several datasets and outperform several existing pruning approaches in both test accuracy and compression ratio.
- Logarithmic Pruning is All You Need. [[paper]](https://arxiv.org/abs/2006.12156)
- Laurent Orseau, Marcus Hutter, Omar Rivasplata. *NeurIPS 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest The Lottery Ticket Hypothesis is a conjecture that every large neural network contains a subnetwork that, when trained in isolation, achieves comparable performance to the large network. An even stronger conjecture has been proven recently: Every sufficiently overparameterized network contains a subnetwork that, at random initialization, but without training, achieves comparable accuracy to the trained large network. This latter result, however, relies on a number of strong assumptions and guarantees a polynomial factor on the size of the large network compared to the target function. In this work, we remove the most limiting assumptions of this previous work while providing significantly tighter bounds:the overparameterized network only needs a logarithmic factor (in all variables but depth) number of neurons per weight of the target subnetwork.
- Exploring Weight Importance and Hessian Bias in Model Pruning. [[paper]](https://arxiv.org/abs/2006.10903)
- Mingchen Li, Yahya Sattar, Christos Thrampoulidis, Samet Oymak.
- Key Word: Lottery Ticket Hypothesis.
- Digest Model pruning is an essential procedure for building compact and computationally-efficient machine learning models. A key feature of a good pruning algorithm is that it accurately quantifies the relative importance of the model weights. While model pruning has a rich history, we still don't have a full grasp of the pruning mechanics even for relatively simple problems involving linear models or shallow neural nets. In this work, we provide a principled exploration of pruning by building on a natural notion of importance.
- Progressive Skeletonization: Trimming more fat from a network at initialization. [[paper]](https://arxiv.org/abs/2006.09081) [[code]](https://github.com/naver/force)
- Pau de Jorge, Amartya Sanyal, Harkirat S. Behl, Philip H.S. Torr, Gregory Rogez, Puneet K. Dokania. *ICLR 2021*
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent studies have shown that skeletonization (pruning parameters) of networks at initialization provides all the practical benefits of sparsity both at inference and training time, while only marginally degrading their performance. However, we observe that beyond a certain level of sparsity (approx 95%), these approaches fail to preserve the network performance, and to our surprise, in many cases perform even worse than trivial random pruning. To this end, we propose an objective to find a skeletonized network with maximum foresight connection sensitivity (FORCE) whereby the trainability, in terms of connection sensitivity, of a pruned network is taken into consideration.
- Pruning neural networks without any data by iteratively conserving synaptic flow. [[paper]](https://arxiv.org/abs/2006.05467) [[code]](https://github.com/ganguli-lab/Synaptic-Flow)
- Hidenori Tanaka, Daniel Kunin, Daniel L. K. Yamins, Surya Ganguli.
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent works have identified, through an expensive sequence of training and pruning cycles, the existence of winning lottery tickets or sparse trainable subnetworks at initialization. This raises a foundational question: can we identify highly sparse trainable subnetworks at initialization, without ever training, or indeed without ever looking at the data? We provide an affirmative answer to this question through theory driven algorithm design.
- Finding trainable sparse networks through Neural Tangent Transfer. [[paper]](https://arxiv.org/abs/2006.08228) [[code]](https://github.com/fmi-basel/neural-tangent-transfer)
- Tianlin Liu, Friedemann Zenke. *ICML 2020*
- Key Word: Lottery Ticket Hypothesis; Neural Tangent Kernel.
- Digest We introduce Neural Tangent Transfer, a method that instead finds trainable sparse networks in a label-free manner. Specifically, we find sparse networks whose training dynamics, as characterized by the neural tangent kernel, mimic those of dense networks in function space. Finally, we evaluate our label-agnostic approach on several standard classification tasks and show that the resulting sparse networks achieve higher classification performance while converging faster.
- What is the State of Neural Network Pruning? [[paper]](https://arxiv.org/abs/2003.03033) [[code]](https://github.com/jjgo/shrinkbench)
- Davis Blalock, Jose Javier Gonzalez Ortiz, Jonathan Frankle, John Guttag. *MLSys 2020*
- Key Word: Lottery Ticket Hypothesis; Survey.
- Digest Neural network pruning---the task of reducing the size of a network by removing parameters---has been the subject of a great deal of work in recent years. We provide a meta-analysis of the literature, including an overview of approaches to pruning and consistent findings in the literature. After aggregating results across 81 papers and pruning hundreds of models in controlled conditions, our clearest finding is that the community suffers from a lack of standardized benchmarks and metrics. This deficiency is substantial enough that it is hard to compare pruning techniques to one another or determine how much progress the field has made over the past three decades. To address this situation, we identify issues with current practices, suggest concrete remedies, and introduce ShrinkBench, an open-source framework to facilitate standardized evaluations of pruning methods.
- Comparing Rewinding and Fine-tuning in Neural Network Pruning. [[paper]](https://arxiv.org/abs/2003.02389) [[code]](https://github.com/lottery-ticket/rewinding-iclr20-public)
- Alex Renda, Jonathan Frankle, Michael Carbin. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We compare fine-tuning to alternative retraining techniques. Weight rewinding (as proposed by Frankle et al., (2019)), rewinds unpruned weights to their values from earlier in training and retrains them from there using the original training schedule. Learning rate rewinding (which we propose) trains the unpruned weights from their final values using the same learning rate schedule as weight rewinding. Both rewinding techniques outperform fine-tuning, forming the basis of a network-agnostic pruning algorithm that matches the accuracy and compression ratios of several more network-specific state-of-the-art techniques.
- Good Subnetworks Provably Exist: Pruning via Greedy Forward Selection. [[paper]](https://arxiv.org/abs/2003.01794) [[code]](https://github.com/lushleaf/Network-Pruning-Greedy-Forward-Selection)
- Mao Ye, Chengyue Gong, Lizhen Nie, Denny Zhou, Adam Klivans, Qiang Liu. *ICML 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest Recent empirical works show that large deep neural networks are often highly redundant and one can find much smaller subnetworks without a significant drop of accuracy. However, most existing methods of network pruning are empirical and heuristic, leaving it open whether good subnetworks provably exist, how to find them efficiently, and if network pruning can be provably better than direct training using gradient descent. We answer these problems positively by proposing a simple greedy selection approach for finding good subnetworks, which starts from an empty network and greedily adds important neurons from the large network.
- The Early Phase of Neural Network Training. [[paper]](https://arxiv.org/abs/2002.10365) [[code]](https://github.com/facebookresearch/open_lth)
- Jonathan Frankle, David J. Schwab, Ari S. Morcos. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We find that, within this framework, deep networks are not robust to reinitializing with random weights while maintaining signs, and that weight distributions are highly non-independent even after only a few hundred iterations.
- Robust Pruning at Initialization. [[paper]](https://arxiv.org/abs/2002.08797)
- Soufiane Hayou, Jean-Francois Ton, Arnaud Doucet, Yee Whye Teh.
- Key Word: Lottery Ticket Hypothesis.
- Digest we provide a comprehensive theoretical analysis of Magnitude and Gradient based pruning at initialization and training of sparse architectures. This allows us to propose novel principled approaches which we validate experimentally on a variety of NN architectures.
- Picking Winning Tickets Before Training by Preserving Gradient Flow. [[paper]](https://arxiv.org/abs/2002.07376) [[code]](https://github.com/alecwangcq/GraSP)
- Chaoqi Wang, Guodong Zhang, Roger Grosse. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We aim to prune networks at initialization, thereby saving resources at training time as well. Specifically, we argue that efficient training requires preserving the gradient flow through the network. This leads to a simple but effective pruning criterion we term Gradient Signal Preservation (GraSP).
- Lookahead: A Far-Sighted Alternative of Magnitude-based Pruning. [[paper]](https://arxiv.org/abs/2002.04809) [[code]](https://github.com/alinlab/lookahead_pruning)
- Sejun Park, Jaeho Lee, Sangwoo Mo, Jinwoo Shin. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest Magnitude-based pruning is one of the simplest methods for pruning neural networks. Despite its simplicity, magnitude-based pruning and its variants demonstrated remarkable performances for pruning modern architectures. Based on the observation that magnitude-based pruning indeed minimizes the Frobenius distortion of a linear operator corresponding to a single layer, we develop a simple pruning method, coined lookahead pruning, by extending the single layer optimization to a multi-layer optimization.
### Lottery Ticket Hypothesis: 2019
- Linear Mode Connectivity and the Lottery Ticket Hypothesis. [[paper]](https://arxiv.org/abs/1912.05671)
- Jonathan Frankle, Gintare Karolina Dziugaite, Daniel M. Roy, Michael Carbin. *ICML 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We study whether a neural network optimizes to the same, linearly connected minimum under different samples of SGD noise (e.g., random data order and augmentation). We find that standard vision models become stable to SGD noise in this way early in training. From then on, the outcome of optimization is determined to a linearly connected region. We use this technique to study iterative magnitude pruning (IMP), the procedure used by work on the lottery ticket hypothesis to identify subnetworks that could have trained in isolation to full accuracy.
- What's Hidden in a Randomly Weighted Neural Network? [[paper]](https://arxiv.org/abs/1911.13299) [[code]](https://github.com/allenai/hidden-networks)
- Vivek Ramanujan, Mitchell Wortsman, Aniruddha Kembhavi, Ali Farhadi, Mohammad Rastegari. *CVPR 2020*
- Key Word: Lottery Ticket Hypothesis; Neural Architecture Search; Weight Agnositic Neural Networks.
- Digest Hidden in a randomly weighted Wide ResNet-50 we show that there is a subnetwork (with random weights) that is smaller than, but matches the performance of a ResNet-34 trained on ImageNet. Not only do these "untrained subnetworks" exist, but we provide an algorithm to effectively find them.
- Drawing Early-Bird Tickets: Towards More Efficient Training of Deep Networks. [[paper]](https://arxiv.org/abs/1909.11957) [[code]](https://github.com/RICE-EIC/Early-Bird-Tickets)
- Haoran You, Chaojian Li, Pengfei Xu, Yonggan Fu, Yue Wang, Xiaohan Chen, Richard G. Baraniuk, Zhangyang Wang, Yingyan Lin. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We discover for the first time that the winning tickets can be identified at the very early training stage, which we term as early-bird (EB) tickets, via low-cost training schemes (e.g., early stopping and low-precision training) at large learning rates. Our finding of EB tickets is consistent with recently reported observations that the key connectivity patterns of neural networks emerge early.
- Rigging the Lottery: Making All Tickets Winners. [[paper]](https://arxiv.org/abs/1911.11134) [[code]](https://github.com/google-research/rigl)
- Utku Evci, Trevor Gale, Jacob Menick, Pablo Samuel Castro, Erich Elsen. *ICML 2020*
- Key Word: Lottery Ticket Hypothesis.
- Digest We introduce a method to train sparse neural networks with a fixed parameter count and a fixed computational cost throughout training, without sacrificing accuracy relative to existing dense-to-sparse training methods. Our method updates the topology of the sparse network during training by using parameter magnitudes and infrequent gradient calculations. We show that this approach requires fewer floating-point operations (FLOPs) to achieve a given level of accuracy compared to prior techniques.
- The Difficulty of Training Sparse Neural Networks. [[paper]](https://arxiv.org/abs/1906.10732)
- Utku Evci, Fabian Pedregosa, Aidan Gomez, Erich Elsen.
- Key Word: Pruning.
- Digest We investigate the difficulties of training sparse neural networks and make new observations about optimization dynamics and the energy landscape within the sparse regime. Recent work of has shown that sparse ResNet-50 architectures trained on ImageNet-2012 dataset converge to solutions that are significantly worse than those found by pruning. We show that, despite the failure of optimizers, there is a linear path with a monotonically decreasing objective from the initialization to the "good" solution.
- A Signal Propagation Perspective for Pruning Neural Networks at Initialization. [[paper]](https://arxiv.org/abs/1906.06307) [[code]](https://github.com/namhoonlee/spp-public)
- Namhoon Lee, Thalaiyasingam Ajanthan, Stephen Gould, Philip H. S. Torr. *ICLR 2020*
- Key Word: Lottery Ticket Hypothesis; Mean Field Theory.
- Digest In this work, by noting connection sensitivity as a form of gradient, we formally characterize initialization conditions to ensure reliable connection sensitivity measurements, which in turn yields effective pruning results. Moreover, we analyze the signal propagation properties of the resulting pruned networks and introduce a simple, data-free method to improve their trainability.
- One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers. [[paper]](https://arxiv.org/abs/1906.02773)
- Ari S. Morcos, Haonan Yu, Michela Paganini, Yuandong Tian. *NeurIPS 2019*
- Key Word: Lottery Ticket Hypothesis.
- Digest Perhaps surprisingly, we found that, within the natural images domain, winning ticket initializations generalized across a variety of datasets, including Fashion MNIST, SVHN, CIFAR-10/100, ImageNet, and Places365, often achieving performance close to that of winning tickets generated on the same dataset.
- Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask. [[paper]](https://arxiv.org/abs/1905.01067) [[code]](https://github.com/uber-research/deconstructing-lottery-tickets)
- Hattie Zhou, Janice Lan, Rosanne Liu, Jason Yosinski. *NeurIPS 2019*
- Key Word: Lottery Ticket Hypothesis.
- Digest In this paper, we have studied how three components to LT-style network pruning—mask criterion, treatment of kept weights during retraining (mask-1 action), and treatment of pruned weights during retraining (mask-0 action)—come together to produce sparse and performant subnetworks.
- The State of Sparsity in Deep Neural Networks. [[paper]](https://arxiv.org/abs/1902.09574) [[code]](https://github.com/ars-ashuha/variational-dropout-sparsifies-dnn)
- Trevor Gale, Erich Elsen, Sara Hooker.
- Key Word: Lottery Ticket Hypothesis.
- Digest We rigorously evaluate three state-of-the-art techniques for inducing sparsity in deep neural networks on two large-scale learning tasks: Transformer trained on WMT 2014 English-to-German, and ResNet-50 trained on ImageNet. Across thousands of experiments, we demonstrate that complex techniques (Molchanov et al., 2017; Louizos et al., 2017b) shown to yield high compression rates on smaller datasets perform inconsistently, and that simple magnitude pruning approaches achieve comparable or better results.
### Lottery Ticket Hypothesis: 2018
- SNIP: Single-shot Network Pruning based on Connection Sensitivity. [[paper]](https://arxiv.org/abs/1810.02340) [[code]](https://github.com/namhoonlee/snip-public)
- Namhoon Lee, Thalaiyasingam Ajanthan, Philip H. S. Torr. *ICLR 2019*
- Key Word: Lottery Ticket Hypothesis.
- Digest In this work, we present a new approach that prunes a given network once at initialization prior to training. To achieve this, we introduce a saliency criterion based on connection sensitivity that identifies structurally important connections in the network for the given task.
- The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. [[paper]](https://arxiv.org/abs/1803.03635) [[code]](https://github.com/google-research/lottery-ticket-hypothesis)
- Jonathan Frankle, Michael Carbin *ICLR 2019*
- Key Word: Lottery Ticket Hypothesis.
- Digest We find that a standard pruning technique naturally uncovers subnetworks whose initializations made them capable of training effectively. Based on these results, we articulate the "lottery ticket hypothesis:" dense, randomly-initialized, feed-forward networks contain subnetworks ("winning tickets") that - when trained in isolation - reach test accuracy comparable to the original network in a similar number of iterations.
## Emergence and Phase Transitions

### Emergence and Phase Transitions: 2025
- Measuring AI Ability to Complete Long Tasks. [[paper]](https://arxiv.org/abs/2503.14499)
- Thomas Kwa, Ben West, Joel Becker, Amy Deng, Katharyn Garcia, Max Hasin, Sami Jawhar, Megan Kinniment, Nate Rush, Sydney Von Arx, Ryan Bloom, Thomas Broadley, Haoxing Du, Brian Goodrich, Nikola Jurkovic, Luke Harold Miles, Seraphina Nix, Tao Lin, Neev Parikh, David Rein, Lucas Jun Koba Sato, Hjalmar Wijk, Daniel M. Ziegler, Elizabeth Barnes, Lawrence Chan.
- Key Word: Agent Training; Compute Scaling.
- Digest The paper introduces a new metric, the 50%-task-completion time horizon, which measures how long humans typically take to complete tasks that AI models achieve with a 50% success rate. Using benchmarks like RE-Bench, HCAST, and 66 novel tasks, the study finds that frontier AI models (e.g., Claude 3.7 Sonnet) have a 50% time horizon of ~50 minutes. AI time horizons have been doubling every ~7 months since 2019, with potential acceleration in 2024, driven by improvements in reliability, adaptability, logical reasoning, and tool use. The authors discuss the external validity of their results and the risks of increased AI autonomy, predicting that if trends hold, AI could automate many software tasks requiring a month of human effort within five years.
- (Mis)Fitting: A Survey of Scaling Laws. [[paper]](https://arxiv.org/abs/2502.18969)
- Margaret Li, Sneha Kudugunta, Luke Zettlemoyer.
- Key Word: Neural Scaling Laws; Survey.
- Digest The paper critiques the reliance on scaling laws in foundation models, highlighting how variations in training setups, architectures, and optimization methods can impact the conclusions drawn from these laws. It discusses discrepancies in prior research on topics like the optimal token-to-parameter ratio and presents an analysis of how small changes can significantly alter results. The paper also surveys over 50 studies on scaling trends, noting that most use power laws but fail to report essential details for reproducibility. To address this, the authors propose a checklist for scaling law research contributors.
- A ghost mechanism: An analytical model of abrupt learning. [[paper]](https://arxiv.org/abs/2501.02378)
- Fatih Dinc, Ege Cirakman, Yiqi Jiang, Mert Yuksekgonul, Mark J. Schnitzer, Hidenori Tanaka.
- Key Word: Abrupt Learning; Learning Dynamics.
- Digest This paper explores the phenomenon of abrupt learning in neural networks, where performance suddenly improves after prolonged stagnation. Using a minimal dynamical system trained on a delayed-activation task, the authors analytically demonstrate that abrupt learning arises from ghost points—destabilizing features in the learning dynamics—rather than bifurcations. They identify a critical learning rate shaped by two loss landscape features: a no-learning zone and an oscillatory minimum. Testing recurrent neural networks (RNNs), they confirm that ghost points precede abrupt learning and destabilize the process. To mitigate this, they propose two strategies: lowering model output confidence to escape no-learning zones and increasing model redundancy (trainable ranks) for stability. This work highlights a bifurcation-free mechanism of abrupt learning and emphasizes the roles of uncertainty and redundancy in stabilizing learning trajectories.
### Emergence and Phase Transitions: 2024
- The Complexity Dynamics of Grokking. [[paper]](https://arxiv.org/abs/2412.09810)
- Branton DeMoss, Silvia Sapora, Jakob Foerster, Nick Hawes, Ingmar Posner.
- Key Word: Grokking; Generalization; Minimum Description Length Principle.
- Digest This paper explores generalization in neural networks through the lens of compression, focusing on the phenomenon of grokking—where networks transition from memorization to generalization after overfitting. The authors introduce a novel intrinsic complexity measure based on Kolmogorov complexity, revealing a consistent rise-and-fall pattern in complexity during training that corresponds to memorization and generalization phases. Leveraging insights from rate-distortion theory and the minimum description length principle, they propose a new regularization method that penalizes spectral entropy to promote low-rank representations. This approach improves generalization and achieves superior dataset compression compared to baseline methods.
- Context-Scaling versus Task-Scaling in In-Context Learning. [[paper]](https://arxiv.org/abs/2410.12783)
- Amirhesam Abedsoltan, Adityanarayanan Radhakrishnan, Jingfeng Wu, Mikhail Belkin.
- Key Word: In-Context Learning; Task-Scaling; Context-Scaling.
- Digest This paper analyzes two key aspects of In-Context Learning (ICL) in transformers: (1) context-scaling, where performance improves with more in-context examples, and (2) task-scaling, where performance improves with more pre-training tasks. The authors show that while transformers achieve both, standard MLPs only achieve task-scaling. To understand context-scaling, they propose a simplified transformer without key, query, value weights, which performs comparably to GPT-2 in various tasks. They find that a data-dependent feature map enables context-scaling, and when combined with an MLP, it achieves both context and task-scaling, offering a simpler framework to study ICL.
- A Hitchhiker's Guide to Scaling Law Estimation. [[paper]](https://arxiv.org/abs/2410.11840)
- Leshem Choshen, Yang Zhang, Jacob Andreas.
- Key Word: Neural scaling Law.
- Digest The paper investigates how to best estimate and interpret scaling laws that predict machine learning model performance. By analyzing a large dataset of losses and evaluations from 485 pretrained models, the authors estimate over 1000 scaling laws. They propose best practices, such as using intermediate training checkpoints and comparing models of similar sizes, to improve prediction accuracy. While models of different families may show variable scaling behavior, predictions can often be made using scaling estimates from related models. Additionally, training multiple small models can be more effective than training a single large one due to seed variability.
- Grokking at the Edge of Linear Separability. [[paper]](https://arxiv.org/abs/2410.04489)
- Alon Beck, Noam Levi, Yohai Bar-Sinai.
- Key Word: Grokking.
- Digest This paper investigates the generalization properties of binary logistic classification and the phenomenon of grokking—delayed generalization with non-monotonic test loss. The authors study a random feature model and show that grokking is amplified when the training set is nearly linearly separable. They prove that if the data is linearly separable from the origin, the model overfits due to the implicit bias of logistic loss. However, for non-separable data, the model generalizes perfectly asymptotically, though early overfitting can occur. The study also finds that near the transition to linear separability, the model can overfit for extended periods before generalizing, drawing parallels to critical phenomena in physical systems.
- Information-Theoretic Foundations for Neural Scaling Laws. [[paper]](https://arxiv.org/abs/2407.01456)
- Hong Jun Jeon, Benjamin Van Roy.
- Key Word: Information Theory; Neural Scaling Laws.
- Digest This paper develops rigorous information-theoretic foundations for neural scaling laws, which describe how out-of-sample error depends on model and dataset size. The authors find that for data generated by an infinitely wide two-layer neural network, the optimal relationship between data and model size is linear, up to logarithmic factors. These findings support large-scale empirical observations and aim to clarify and guide future research in neural scaling laws.
### Emergence and Phase Transitions: 2023
- More is Better in Modern Machine Learning: when Infinite Overparameterization is Optimal and Overfitting is Obligatory. [[paper]](https://arxiv.org/abs/2311.14646)
- James B. Simon, Dhruva Karkada, Nikhil Ghosh, Mikhail Belkin.
- Key Word: Overparameterization; Random Feature Regression.
- Digest This paper highlights the empirical observation that larger model size, more data, and more computation improve performance in deep learning. The paper provides theoretical backing to these observations by showing that these properties hold in random feature regression, equivalent to shallow networks with only the last layer trained. The study demonstrates that the test risk of random feature regression decreases with the number of features and samples, implying that infinite width random feature architectures are preferable. Additionally, it emphasizes the importance of training to near-zero training loss for achieving near-optimal performance, especially for tasks characterized by power law eigenstructure. The findings suggest the benefits of overparameterization, overfitting, and more data in random feature models.
- Grokking as the Transition from Lazy to Rich Training Dynamics. [[paper]](https://arxiv.org/abs/2310.06110)
- Tanishq Kumar, Blake Bordelon, Samuel J. Gershman, Cengiz Pehlevan.
- Key Word: Grokking; Kernel Dynamics; Feature Learning.
- Digest The paper explores the phenomenon of "grokking" in neural networks, where the training loss decreases much earlier than the test loss. It suggests that grokking occurs as neural networks transition from lazy training dynamics to rich feature learning. The study uses a simple polynomial regression problem with a two-layer neural network to illustrate this mechanism and identifies key factors contributing to grokking. These factors include the rate of feature learning, alignment of initial features with the target function, dataset size, and the network's initial training regime. The paper argues that this transition from lazy to rich training dynamics can also impact grokking in more general settings, such as MNIST, one-layer Transformers, and student-teacher networks.
- Droplets of Good Representations: Grokking as a First Order Phase Transition in Two Layer Networks. [[paper]](https://arxiv.org/abs/2310.03789)
- Noa Rubin, Inbar Seroussi, Zohar Ringel.
- Key Word: Grokking.
- Digest This paper explores the phenomenon of Grokking in deep neural networks (DNNs) and its connection to feature learning. It applies the adaptive kernel approach to two teacher-student models and provides analytical predictions on feature learning and Grokking properties. The paper suggests that Grokking in DNNs is akin to a phase transition, resulting in distinct internal representations of the teacher after the transition.
- Explaining grokking through circuit efficiency. [[paper]](https://arxiv.org/abs/2309.02390)
- Vikrant Varma, Rohin Shah, Zachary Kenton, János Kramár, Ramana Kumar.
- Key Word: Grokking.
- Digest This paper addresses the phenomenon of "grokking" in neural networks, where a network initially achieves perfect training accuracy but poor generalization. The authors propose that grokking happens when a task allows both a generalizing solution (slower but more efficient) and a memorizing solution. They suggest that memorization becomes less efficient with larger training datasets, while generalization remains unaffected. This implies a critical dataset size where both approaches become equally efficient. The paper makes and confirms four novel predictions about grokking, including the surprising observations of "ungrokking" (regression from perfect to low test accuracy) and "semi-grokking" (delayed generalization to partial test accuracy).
- Scaling Laws Do Not Scale. [[paper]](https://arxiv.org/abs/2307.03201)
- Fernando Diaz, Michael Madaio.
- Key Word: Neural Scaling Laws.
- Digest This papepr challenges the notion of scaling laws in artificial intelligence (AI) models, arguing that as dataset sizes increase, the diverse values and preferences of different communities represented in the data may not align with the metrics used to evaluate model performance.
- Absorbing Phase Transitions in Artificial Deep Neural Networks. [[paper]](https://arxiv.org/abs/2307.02284)
- Keiichi Tamai, Tsuyoshi Okubo, Truong Vinh Truong Duy, Naotake Natori, Synge Todo.
- Key Word: Phase Transitions; Neural Scaling Laws.
- Digest This paper presents a framework for understanding the behavior of finite artificial deep neural networks by drawing parallels to universal critical phenomena in absorbing phase transitions. The authors investigate order-to-chaos transitions in fully-connected feedforward and convolutional neural networks, demonstrating that these transitions exist even in finite networks and that the architecture influences the universality class of the transition. Finite-size scaling is also successfully applied, allowing for a semi-quantitative description of signal propagation dynamics.
- The Underlying Scaling Laws and Universal Statistical Structure of Complex Datasets. [[paper]](https://arxiv.org/abs/2306.14975)
- Noam Levi, Yaron Oz.
- Key Word: Neural Scaling Laws; Random Matrix Theory.
- Digest The paper explores the underlying scaling laws and universal statistical structure of complex datasets, using tools from statistical physics and Random Matrix Theory (RMT). They analyze the feature-feature covariance matrix and observe that the power-law scalings of eigenvalues differ between uncorrelated random data and real-world data. They find that introducing long-range correlations can recover the scaling behavior in synthetic data, and both synthetic and real-world datasets belong to the same universality class as chaotic systems rather than integrable systems. The expected RMT statistical behavior is evident in empirical covariance matrices at smaller dataset sizes than traditionally used for training, and it can be related to the number of samples needed to approximate the population power-law scaling behavior.
- Hidden symmetries of ReLU networks. [[paper]](https://arxiv.org/abs/2306.06179)
- J. Elisenda Grigsby, Kathryn Lindsey, David Rolnick. *ICML 2023*
- Key Word: Permutation Symmetries.
- Digest The paper explores the representation of feedforward ReLU neural networks using their parameter space during training, investigating the existence of hidden symmetries that result in different parameter settings producing the same function. The authors prove that networks without narrow layers have parameter settings without hidden symmetries. They also identify mechanisms that lead to hidden symmetries and conduct experiments indicating that the probability of networks having no hidden symmetries decreases as depth increases, but increases as width and input dimension increase.
- Are Emergent Abilities of Large Language Models a Mirage? [[paper]](https://arxiv.org/abs/2304.15004)
- Rylan Schaeffer, Brando Miranda, Sanmi Koyejo.
- Key Word: Large Language Models; Neural Scaling Laws; Emergent Abilities.
- Digest Recent work claims that large language models display emergent abilities, abilities not present in smaller-scale models that are present in larger-scale models. What makes emergent abilities intriguing is two-fold: their sharpness, transitioning seemingly instantaneously from not present to present, and their unpredictability, appearing at seemingly unforeseeable model scales. Here, we present an alternative explanation for emergent abilities: that for a particular task and model family, when analyzing fixed model outputs, one can choose a metric which leads to the inference of an emergent ability or another metric which does not. We find strong supporting evidence that emergent abilities may not be a fundamental property of scaling AI models.
- Data pruning and neural scaling laws: fundamental limitations of score-based algorithms. [[paper]](https://arxiv.org/abs/2302.06960)
- Fadhel Ayed, Soufiane Hayou.
- Key Word: Data Pruning; Neural Scaling Laws.
- Digest In this work, we focus on score-based data pruning algorithms and show theoretically and empirically why such algorithms fail in the high compression regime. We demonstrate ``No Free Lunch" theorems for data pruning and present calibration protocols that enhance the performance of existing pruning algorithms in this high compression regime using randomization.
- Progress measures for grokking via mechanistic interpretability. [[paper]](https://arxiv.org/abs/2301.05217)
- Neel Nanda, Lawrence Chan, Tom Liberum, Jess Smith, Jacob Steinhardt.
- Key Work: Grokking; Interpretability.
- Digest We argue that progress measures can be found via mechanistic interpretability: reverse-engineering learned behaviors into their individual components. As a case study, we investigate the recently-discovered phenomenon of ``grokking'' exhibited by small transformers trained on modular addition tasks.
- Grokking modular arithmetic. [[paper]](https://arxiv.org/abs/2301.02679)
- Andrey Gromov.
- Key Word: Grokking; Modular Addition; Interpretability.
- Digest We present a simple neural network that can learn modular arithmetic tasks and exhibits a sudden jump in generalization known as ``grokking''. Concretely, we present (i) fully-connected two-layer networks that exhibit grokking on various modular arithmetic tasks under vanilla gradient descent with the MSE loss function in the absence of any regularization.
### Emergence and Phase Transitions: 2022
- Feature learning in neural networks and kernel machines that recursively learn features. [[paper]](https://arxiv.org/abs/2212.13881) [[code]](https://github.com/aradha/recursive_feature_machines)
- Adityanarayanan Radhakrishnan, Daniel Beaglehole, Parthe Pandit, Mikhail Belkin.
- Key Word: Feature Learning; Kernel Machines; Grokking; Lottery Ticket Hypothesis.
- Digest We isolate the key mechanism driving feature learning in fully connected neural networks by connecting neural feature learning to the average gradient outer product. We subsequently leverage this mechanism to design Recursive Feature Machines (RFMs), which are kernel machines that learn features. We show that RFMs (1) accurately capture features learned by deep fully connected neural networks, (2) close the gap between kernel machines and fully connected networks, and (3) surpass a broad spectrum of models including neural networks on tabular data.
- Grokking phase transitions in learning local rules with gradient descent. [[paper]](https://arxiv.org/abs/2210.15435)
- Bojan Žunkovič, Enej Ilievski.
- Key Word: Tensor Network; Grokking; Many-Body Quantum Mechanics; Neural Collapse.
- Digest We discuss two solvable grokking (generalisation beyond overfitting) models in a rule learning scenario. We show that grokking is a phase transition and find exact analytic expressions for the critical exponents, grokking probability, and grokking time distribution. Further, we introduce a tensor-network map that connects the proposed grokking setup with the standard (perceptron) statistical learning theory and show that grokking is a consequence of the locality of the teacher model. As an example, we analyse the cellular automata learning task, numerically determine the critical exponent and the grokking time distributions and compare them with the prediction of the proposed grokking model. Finally, we numerically analyse the connection between structure formation and grokking.
- Broken Neural Scaling Laws. [[paper]](https://arxiv.org/abs/2210.14891) [[code]](https://github.com/ethancaballero/broken_neural_scaling_laws)
- Ethan Caballero, Kshitij Gupta, Irina Rish, David Krueger.
- Key Word: Neural Scaling Laws.
- Digest We present a smoothly broken power law functional form that accurately models and extrapolates the scaling behaviors of deep neural networks (i.e. how the evaluation metric of interest varies as the amount of compute used for training, number of model parameters, or training dataset size varies) for each task within a large and diverse set of upstream and downstream tasks, in zero-shot, prompted, and fine-tuned settings. This set includes large-scale vision and unsupervised language tasks, diffusion generative modeling of images, arithmetic, and reinforcement learning.
- How Much Data Are Augmentations Worth? An Investigation into Scaling Laws, Invariance, and Implicit Regularization. [[paper]](https://arxiv.org/abs/2210.06441) [[code]](https://github.com/JonasGeiping/dataaugs)
- Jonas Geiping, Micah Goldblum, Gowthami Somepalli, Ravid Shwartz-Ziv, Tom Goldstein, Andrew Gordon Wilson.
- Key Word: Data Augmentation; Neural Scaling Laws; Implicit Regularization.
- Digest Despite the clear performance benefits of data augmentations, little is known about why they are so effective. In this paper, we disentangle several key mechanisms through which data augmentations operate. Establishing an exchange rate between augmented and additional real data, we find that in out-of-distribution testing scenarios, augmentations which yield samples that are diverse, but inconsistent with the data distribution can be even more valuable than additional training data.
- Omnigrok: Grokking Beyond Algorithmic Data. [[paper]](https://arxiv.org/abs/2210.01117)
- Ziming Liu, Eric J. Michaud, Max Tegmark.
- Key Word: Grokking Dynamics.
- Digest Grokking, the unusual phenomenon for algorithmic datasets where generalization happens long after overfitting the training data, has remained elusive. We aim to understand grokking by analyzing the loss landscapes of neural networks, identifying the mismatch between training and test losses as the cause for grokking. We refer to this as the "LU mechanism" because training and test losses (against model weight norm) typically resemble "L" and "U", respectively. This simple mechanism can nicely explain many aspects of grokking: data size dependence, weight decay dependence, the emergence of representations, etc.
- Revisiting Neural Scaling Laws in Language and Vision. [[paper]](https://arxiv.org/abs/2209.06640)
- Ibrahim Alabdulmohsin, Behnam Neyshabur, Xiaohua Zhai.
- Key Word: Neural Scaling Laws; Multi-modal Learning.
- Digest The remarkable progress in deep learning in recent years is largely driven by improvements in scale, where bigger models are trained on larger datasets for longer schedules. To predict the benefit of scale empirically, we argue for a more rigorous methodology based on the extrapolation loss, instead of reporting the best-fitting (interpolating) parameters. We then present a recipe for estimating scaling law parameters reliably from learning curves. We demonstrate that it extrapolates more accurately than previous methods in a wide range of architecture families across several domains, including image classification, neural machine translation (NMT) and language modeling, in addition to tasks from the BIG-Bench evaluation benchmark.
- On the Principles of Parsimony and Self-Consistency for the Emergence of Intelligence. [[paper]](https://arxiv.org/abs/2207.04630)
- Yi Ma, Doris Tsao, Heung-Yeung Shum.
- Key Word: Intelligence; Parsimony; Self-Consistency; Rate Reduction.
- Digest Ten years into the revival of deep networks and artificial intelligence, we propose a theoretical framework that sheds light on understanding deep networks within a bigger picture of Intelligence in general. We introduce two fundamental principles, Parsimony and Self-consistency, that we believe to be cornerstones for the emergence of Intelligence, artificial or natural. While these two principles have rich classical roots, we argue that they can be stated anew in entirely measurable and computable ways.
- Synergy and Symmetry in Deep Learning: Interactions between the Data, Model, and Inference Algorithm. [[paper]](https://arxiv.org/abs/2207.04612)
- Lechao Xiao, Jeffrey Pennington. *ICML 2022*
- Key Word: Synergy; Symmetry; Implicit Bias; Neural Tangent Kernel; Neural Scaling Laws.
- Digest Although learning in high dimensions is commonly believed to suffer from the curse of dimensionality, modern machine learning methods often exhibit an astonishing power to tackle a wide range of challenging real-world learning problems without using abundant amounts of data. How exactly these methods break this curse remains a fundamental open question in the theory of deep learning. While previous efforts have investigated this question by studying the data (D), model (M), and inference algorithm (I) as independent modules, in this paper, we analyze the triplet (D, M, I) as an integrated system and identify important synergies that help mitigate the curse of dimensionality.
- How Much More Data Do I Need? Estimating Requirements for Downstream Tasks. [[paper]](https://arxiv.org/abs/2207.01725)
- Rafid Mahmood, James Lucas, David Acuna, Daiqing Li, Jonah Philion, Jose M. Alvarez, Zhiding Yu, Sanja Fidler, Marc T. Law. *CVPR 2022*
- Key Word: Neural Scaling Laws; Active Learning.
- Digest Prior work on neural scaling laws suggest that the power-law function can fit the validation performance curve and extrapolate it to larger data set sizes. We find that this does not immediately translate to the more difficult downstream task of estimating the required data set size to meet a target performance. In this work, we consider a broad class of computer vision tasks and systematically investigate a family of functions that generalize the power-law function to allow for better estimation of data requirements.
- Beyond neural scaling laws: beating power law scaling via data pruning. [[paper]](https://arxiv.org/abs/2206.14486)
- Ben Sorscher, Robert Geirhos, Shashank Shekhar, Surya Ganguli, Ari S. Morcos.
- Key Word: Dataset Pruning; Ensemble Active Learning.
- Digest Widely observed neural scaling laws, in which error falls off as a power of the training set size, model size, or both, have driven substantial performance improvements in deep learning. However, these improvements through scaling alone require considerable costs in compute and energy. Here we focus on the scaling of error with dataset size and show how both in theory and practice we can break beyond power law scaling and reduce it to exponential scaling instead if we have access to a high-quality data pruning metric that ranks the order in which training examples should be discarded to achieve any pruned dataset size. We then test this new exponential scaling prediction with pruned dataset size empirically, and indeed observe better than power law scaling performance on ResNets trained on CIFAR-10, SVHN, and ImageNet.
- Exact Phase Transitions in Deep Learning. [[paper]](https://arxiv.org/abs/2205.12510)
- Liu Ziyin, Masahito Ueda.
- Key Word: Phase Transitions; Symmetry Breaking; Mean-Field Analysis; Statistical Physics.
- Digest The paper presents a theory that demonstrates the existence of first-order and second-order phase transitions in deep learning, similar to those observed in statistical physics, by analyzing the interplay between prediction error and model complexity in the training loss. The findings have implications for neural network optimization and shed light on the origin of the posterior collapse problem in Bayesian deep learning.
- Towards Understanding Grokking: An Effective Theory of Representation Learning. [[paper]](https://arxiv.org/abs/2205.10343)
- Ziming Liu, Ouail Kitouni, Niklas Nolte, Eric J. Michaud, Max Tegmark, Mike Williams.
- Key Word: Grokking; Physics of Learning; Deep Double Descent.
- Digest We aim to understand grokking, a phenomenon where models generalize long after overfitting their training set. We present both a microscopic analysis anchored by an effective theory and a macroscopic analysis of phase diagrams describing learning performance across hyperparameters. We find that generalization originates from structured representations whose training dynamics and dependence on training set size can be predicted by our effective theory in a toy setting. We observe empirically the presence of four learning phases: comprehension, grokking, memorization, and confusion.
- Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets. [[paper]](https://arxiv.org/abs/2201.02177) [[code]](https://github.com/openai/grok)
- Alethea Power, Yuri Burda, Harri Edwards, Igor Babuschkin, Vedant Misra.
- Key Word: Grokking; Overfitting.
- Digest In this paper we propose to study generalization of neural networks on small algorithmically generated datasets. In this setting, questions about data efficiency, memorization, generalization, and speed of learning can be studied in great detail. In some situations we show that neural networks learn through a process of "grokking" a pattern in the data, improving generalization performance from random chance level to perfect generalization, and that this improvement in generalization can happen well past the point of overfitting.
### Emergence and Phase Transitions: 2021
- Learning Curve Theory. [[paper]](https://arxiv.org/abs/2102.04074)
- Marcus Hutter.
- Key Word: Neural Scaling Law; Learning Curve Theory.
- Digest Recently a number of empirical "universal" scaling law papers have been published, most notably by OpenAI. `Scaling laws' refers to power-law decreases of training or test error w.r.t. more data, larger neural networks, and/or more compute. In this work we focus on scaling w.r.t. data size n. Theoretical understanding of this phenomenon is largely lacking, except in finite-dimensional models for which error typically decreases with n−1/2 or n−1, where n is the sample size. We develop and theoretically analyse the simplest possible (toy) model that can exhibit n−β learning curves for arbitrary power β>0, and determine whether power laws are universal or depend on the data distribution.
- Explaining Neural Scaling Laws. [[paper]](https://arxiv.org/abs/2102.06701) [[code]](https://github.com/google/neural-tangents)
- Yasaman Bahri, Ethan Dyer, Jared Kaplan, Jaehoon Lee, Utkarsh Sharma. *ICLR 2022*
- Key Word: Scaling Laws; Neural Tangent Kernel.
- Digest We propose a theory that explains and connects these scaling laws. We identify variance-limited and resolution-limited scaling behavior for both dataset and model size, for a total of four scaling regimes. The variance-limited scaling follows simply from the existence of a well-behaved infinite data or infinite width limit, while the resolution-limited regime can be explained by positing that models are effectively resolving a smooth data manifold.
### Emergence and Phase Transitions: 2020
- A Neural Scaling Law from the Dimension of the Data Manifold. [[paper]](https://arxiv.org/abs/2004.10802)
- Utkarsh Sharma, Jared Kaplan.
- Key Word: Neural Scaling Law; Manifold Intrinsic Dimension; Fractal Dimension.
- Digest This paper investigates neural network performance with abundant data, finding that well-trained networks exhibit power-law loss scaling (L∝N−α) based on network parameters (N). The phenomenon applies broadly across diverse data types and scales. The study proposes that this behavior stems from neural models effectively conducting regression on an intrinsic dimension (d) data manifold. The theory predicts α≈4/d scaling exponents for cross-entropy and mean-squared error losses. Empirical validation occurs via independent measurements of intrinsic dimension and scaling exponents in a teacher/student framework, including various d and α values through random teacher network adjustments. CNN classifiers and GPT-style language models further test the theory's applicability across datasets.
## Interactions with Neuroscience
### Interactions with Neuroscience: 2023
- How deep is the brain? The shallow brain hypothesis. [[paper]](https://www.nature.com/articles/s41583-023-00756-z)
- Mototaka Suzuki; Cyriel M. A. Pennartz; Jaan Aru.
- Key Word: Shallow Brain Hypothesis.
- Digest This paper critiques the common assumption in deep learning and predictive coding that neural network inference is hierarchical, pointing out the overlooked neurobiological evidence of direct interactions between all cortical areas and subcortical regions. It challenges the prevalent cortico-centric, hierarchical models in current neural networks, suggesting they miss key computational principles used by the brain. Introducing the "shallow brain hypothesis," the authors propose that hierarchical cortical processing works in tandem with a parallel process significantly involving subcortical areas. They argue this integrated architecture, which leverages the computational abilities of cortical microcircuits and thalamo-cortical loops absent in conventional models, offers crucial advantages for achieving the rapid and flexible computational capabilities seen in mammalian brains.
- Finding Neurons in a Haystack: Case Studies with Sparse Probing. [[paper]](https://arxiv.org/abs/2305.01610) [[code]](https://github.com/wesg52/sparse-probing-paper)
- Wes Gurnee, Neel Nanda, Matthew Pauly, Katherine Harvey, Dmitrii Troitskii, Dimitris Bertsimas.
- Key Word: Probing; Mechanistic Interpretability; Superposition; Sparse Coding.
- Digest We seek to understand how high-level human-interpretable features are represented within the internal neuron activations of LLMs. We train k-sparse linear classifiers (probes) on these internal activations to predict the presence of features in the input; by varying the value of k we study the sparsity of learned representations and how this varies with model scale. With k=1, we localize individual neurons which are highly relevant for a particular feature, and perform a number of case studies to illustrate general properties of LLMs.
### Interactions with Neuroscience: 2022
- Multilevel development of cognitive abilities in an artificial neural network. [[paper]](https://www.pnas.org/doi/abs/10.1073/pnas.2201304119?af=R)
- Konstantin Volzhenin, Jean-Pierre Changeux, Guillaume Dumas. *PNAS*
- Key Word: Global Neuronal Workspace.
- Digest We introduce a three-level computational model of information processing and acquisition of cognitive abilities. We propose minimal architectural requirements to build these levels, and how the parameters affect their performance and relationships. The first sensorimotor level handles local nonconscious processing, here during a visual classification task. The second level or cognitive level globally integrates the information from multiple local processors via long-ranged connections and synthesizes it in a global, but still nonconscious, manner. The third and cognitively highest level handles the information globally and consciously. It is based on the global neuronal workspace (GNW) theory and is referred to as the conscious level.
- Deep Problems with Neural Network Models of Human Vision. [[paper]](https://psyarxiv.com/5zf4s/)
- Jeffrey S BowersGaurav MalhotraMarin DujmovićMilton Llera MonteroChristian TsvetkovValerio BiscioneGuillermo PueblaFederico G AdolfiJohn HummelRachel Flood HeatonBenjamin EvansJeff MitchellRyan Blything.
- Key Word: Brain-Score; Computational Neuroscience; Convolutional Neural Networks; Representational Similarity Analysis.
- Digest We show that the good prediction on these datasets may be mediated by DNNs that share little overlap with biological vision. More problematically, we show that DNNs account for almost no results from psychological research. This contradicts the common claim that DNNs are good, let alone the best, models of human object recognition.
- Reassessing hierarchical correspondences between brain and deep networks through direct interface. [[paper]](https://www.science.org/doi/10.1126/sciadv.abm2219)
- Nicholas J Sexton, Bradley C Love. *Science Advances*
- Key Word: Neural Interfacing Analysis; Shared Neural Variance.
- Digest Functional correspondences between deep convolutional neural networks (DCNNs) and the mammalian visual system support a hierarchical account in which successive stages of processing contain ever higher-level information. However, these correspondences between brain and model activity involve shared, not task-relevant, variance. We propose a stricter account of correspondence: If a DCNN layer corresponds to a brain region, then replacing model activity with brain activity should successfully drive the DCNN’s object recognition decision. Using this approach on three datasets, we found that all regions along the ventral visual stream best corresponded with later model layers, indicating that all stages of processing contained higher-level information about object category.
- Wiring Up Vision: Minimizing Supervised Synaptic Updates Needed to Produce a Primate Ventral Stream. [[paper]](https://openreview.net/forum?id=g1SzIRLQXMM)
- Franziska Geiger, Martin Schrimpf, Tiago Marques, James J. DiCarlo. *ICLR 2022*
- Key Word: Computational Neuroscience; Primate Visual Ventral Stream.
- Digest We develop biologically-motivated initialization and training procedures to train models with 200x fewer synaptic updates (epochs x labeled images x weights) while maintaining 80% of brain predictivity on a set of neural and behavioral benchmarks.
- Curriculum learning as a tool to uncover learning principles in the brain. [[paper]](https://openreview.net/forum?id=TpJMvo0_pu-)
- Daniel R. Kepple, Rainer Engelken, Kanaka Rajan. *ICLR 2022*
- Key Word: Curriculum Learning; Neuroscience.
- Digest We present a novel approach to use curricula to identify principles by which a system learns. Previous work in curriculum learning has focused on how curricula can be designed to improve learning of a model on particular tasks. We consider the inverse problem: what can a curriculum tell us about how a learning system acquired a task? Using recurrent neural networks (RNNs) and models of common experimental neuroscience tasks, we demonstrate that curricula can be used to differentiate learning principles using target-based and a representation-based loss functions as use cases.
- Building Transformers from Neurons and Astrocytes. [[paper]](https://www.biorxiv.org/content/10.1101/2022.10.12.511910v1)
- Leo Kozachkov, Ksenia V. Kastanenka, Dmitry Krotov.
- Key Word: Transformers; Glia; Astrocytes.
- Digest In this work we hypothesize that neuron-astrocyte networks can naturally implement the core computation performed by the Transformer block in AI. The omnipresence of astrocytes in almost any brain area may explain the success of Transformers across a diverse set of information domains and computational tasks.
- High-performing neural network models of visual cortex benefit from high latent dimensionality. [[paper]](https://www.biorxiv.org/content/10.1101/2022.07.13.499969v1)
- Eric Elmoznino, Michael F. Bonner.
- Key Word: Dimensionality and Alignment in Computational Brain Models.
- Digest The prevailing view holds that optimal DNNs compress their representations onto low-dimensional manifolds to achieve invariance and robustness, which suggests that better models of visual cortex should have low-dimensional geometries. Surprisingly, we found a strong trend in the opposite direction—neural networks with high-dimensional image manifolds tend to have better generalization performance when predicting cortical responses to held-out stimuli in both monkey electrophysiology and human fMRI data.
- Constrained Predictive Coding as a Biologically Plausible Model of the Cortical Hierarchy. [[paper]](https://arxiv.org/abs/2210.15752) [[code]](https://github.com/ttesileanu/bio-pcn)
- Siavash Golkar, Tiberiu Tesileanu, Yanis Bahroun, Anirvan M. Sengupta, Dmitri B. Chklovskii. *NeurIPS 2022*
- Key Word: Predictive Coding Theory.
- Digest The paper presents a modified version of the Predictive Coding (PC) framework, called Constrained Predictive Coding, which addresses unresolved issues and controversies in mapping PC onto the cortical hierarchy. The authors introduce a disentangling-inspired constraint on hidden-layer neural activities, derive an upper bound for the PC objective, and optimize it to develop a biologically plausible network that performs as well as the original PC objective.
- Painful intelligence: What AI can tell us about human suffering. [[paper]](https://arxiv.org/abs/2205.15409)
- Aapo Hyvärinen.
- Key Word: Neuroscience.
- Digest This book uses the modern theory of artificial intelligence (AI) to understand human suffering or mental pain. Both humans and sophisticated AI agents process information about the world in order to achieve goals and obtain rewards, which is why AI can be used as a model of the human brain and mind. This book intends to make the theory accessible to a relatively general audience, requiring only some relevant scientific background. The book starts with the assumption that suffering is mainly caused by frustration. Frustration means the failure of an agent (whether AI or human) to achieve a goal or a reward it wanted or expected.
- The developmental trajectory of object recognition robustness: children are like small adults but unlike big deep neural networks. [[paper]](https://arxiv.org/abs/2205.10144) [[code]](https://github.com/wichmann-lab/robustness-development)
- Lukas S. Huber, Robert Geirhos, Felix A. Wichmann.
- Key Word: Object Recognition; Out-of-Distribution Generalization; Children.
- Digest We find, first, that already 4–6 year-olds showed remarkable robustness to image distortions and outperform DNNs trained on ImageNet. Second, we estimated the number of “images” children have been exposed to during their lifetime. Compared to various DNNs, children's high robustness requires relatively little data. Third, when recognizing objects children—like adults but unlike DNNs—rely heavily on shape but not on texture cues. Together our results suggest that the remarkable robustness to distortions emerges early in the developmental trajectory of human object recognition and is unlikely the result of a mere accumulation of experience with distorted visual input.
- Finding Biological Plausibility for Adversarially Robust Features via Metameric Tasks. [[paper]](https://arxiv.org/abs/2202.00838) [[code]](https://github.com/anneharrington/adversarially-robust-periphery)
- Anne Harrington, Arturo Deza. *ICLR 2022*
- Key Word: Adversarial Robustness; Peripheral Computation; Psychophysics.
- Digest To understand how adversarially robust optimizations/representations compare to human vision, we performed a psychophysics experiment using a metamer task where we evaluated how well human observers could distinguish between images synthesized to match adversarially robust representations compared to non-robust representations and a texture synthesis model of peripheral vision. We found that the discriminability of robust representation and texture model images decreased to near chance performance as stimuli were presented farther in the periphery.
### Interactions with Neuroscience: 2021
- Relating transformers to models and neural representations of the hippocampal formation. [[paper]](https://arxiv.org/abs/2112.04035)
- James C.R. Whittington, Joseph Warren, Timothy E.J. Behrens. *ICLR 2022*
- Key Word: Transformers; Hippocampus; Cortex.
- Digest We show that transformers, when equipped with recurrent position encodings, replicate the precisely tuned spatial representations of the hippocampal formation; most notably place and grid cells. Furthermore, we show that this result is no surprise since it is closely related to current hippocampal models from neuroscience.
- Partial success in closing the gap between human and machine vision. [[paper]](https://arxiv.org/abs/2106.07411) [[code]](https://github.com/bethgelab/model-vs-human)
- Robert Geirhos, Kantharaju Narayanappa, Benjamin Mitzkus, Tizian Thieringer, Matthias Bethge, Felix A. Wichmann, Wieland Brendel. *NeurIPS 2021*
- Key Word: Out-of-Distribution Generalization; Psychophysical Experiments.
- Digest A few years ago, the first CNN surpassed human performance on ImageNet. However, it soon became clear that machines lack robustness on more challenging test cases, a major obstacle towards deploying machines "in the wild" and towards obtaining better computational models of human visual perception. Here we ask: Are we making progress in closing the gap between human and machine vision? To answer this question, we tested human observers on a broad range of out-of-distribution (OOD) datasets, recording 85,120 psychophysical trials across 90 participants.
- Does enhanced shape bias improve neural network robustness to common corruptions? [[paper]](https://arxiv.org/abs/2104.09789)
- Chaithanya Kumar Mummadi, Ranjitha Subramaniam, Robin Hutmacher, Julien Vitay, Volker Fischer, Jan Hendrik Metzen. *ICLR 2021*
- Key Word: Shape-Texture; Robustness.
-